Известные всему миру геоглифы плато Наска уже не вызывают у общественности, в том числе научной, практически никакого интереса. Связано это в основном с тем, что официальной наукой, в лице многих исследователей и режиссеров научно-популярных фильмов на эту тему, приложено немало усилий, чтобы убедить всех в том, что рисунки и чертежи этого плато – не что иное, как творчество обкурившихся шаманов. При этом, правда, никак не объясняется, каким образом практически неграмотные во всех областях знаний люди смогли создать то, что требует серьезного технического и, прежде всего, научного подхода к созданию подобных изображений на поверхности с рельефом и таких размеров.

Те немногие попытки объяснить эти геоглифы логически и здраво, которые были предприняты, автоматически отнесены к области фантастических предположений с отодвиганием их на третий план при обсуждении темы.

В данной статье я попытаюсь провести предварительный анализ одного чертежа на плато “Наска Пальпа”. Изображение известно, но не очень распространено в виде фотографий.

Прежде чем начать описание, я хочу выразить свою благодарность Лаборатории Альтернативной Истории и лично А. Склярову за предоставленные для изучения материалы и данные. Также я крайне признателен А. Жукову, который в апреле этого года провел весьма интересную исследовательскую поездку в Перу, благодаря которой мне и посчастливилось познакомиться с данным чертежом.

Итак, изображение расположено на плато “Наска Пальпа” что несколько в отдалении от всемирно известного плато “Наска”. Чертеж, а именно таковым это является на самом деле, выполнен на неровной поверхности неизвестным способом на площади около километра.

Нет никаких сомнений в том, что на самом деле данное изображение уже давно является предметом пристального исследования определенных ученых кругов, о которых они сами никогда просто так не поведают. Тому есть несколько причин.

1. Идеальные геометрические пропорции, создание которых абсолютно невозможно без разработанной правильной системы координат и знания законов геометрии.
2. Уникальная техника исполнения, ставшая просто теоретически возможной для нас лишь в последние лет пятьдесят; но ведь точно известно, что чертежу не менее 1000 лет!
3. Совершенно понятное заключение, что местные аборигены такого создать ни при каких, даже теоретических, условиях не были способны.

Также весьма вероятно, что в чертеже присутствует зашифрованная информация, ключ к открытию которой заключается в длинах, величинах и прочих соотношениях данного чертежа.

Целью моего исследования стало доказательство невозможности случайного совпадения некоторых деталей и закономерностей этого изображения, что автоматически доказывает его нечеловеческое происхождения, т.к. аборигенов мы уже, и справедливо, исключили из списка претендентов на создание подобного шедевра. А человек современный 1000 лет назад начертать подобное никак не мог.

Итак, кто же это создал и что это такое?

На первый вопрос, я думаю, мы ответа, исходя из имеющихся данных, не получим. Разве что обобщенно заявить, что это дело рук разумных существ.

А вот на второй вопрос, ответ весьма интересный. Можно построить как минимум несколько одинаково правильных предположений о назначении этого чертежа.

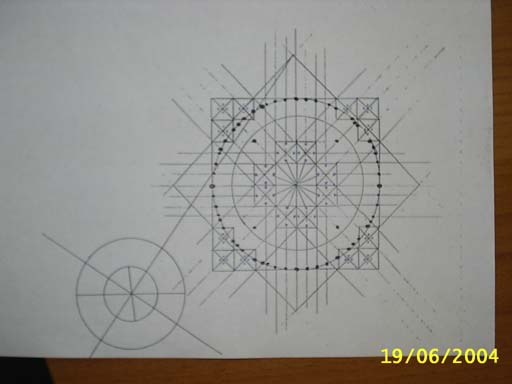
Я попытался поверхностно, насколько позволяют мои личные знания в этой области, исследовать этот рисунок. Прежде всего, я попытался начертить его на обычном листе, дабы воссоздать правильную плоскость. Фото сделано с некоторым наклоном, под углом.

Каково же было мое удивление, когда я понял, что не сумею начертить его просто так. Для того, чтобы чертеж начал получаться геометрически размеренным и правильным, необходимо начать его исключительно из центра. Может, кто-то более искушенный в профессиональном черчении и сумеет, применяя какие то хитрые приемы, это сделать, а я, как современный рядовой абориген не смог.

Но я нашел подсказку. Именно для таких как я и были они сделаны, дабы не нарушить задуманной кем-то гармонии рисунка.

Начертив правильный квадрат с равными сторонами и, без труда найдя в нем центр, я начертил первые восемь квадратов вокруг. Естественно я сразу же разбил их накрест линиями, найдя их центр. И тут я понял, зачем на рисунке четыре точки расположены внутри первого круга. Они абсолютно точно указывают на места соприкосновения квадратов (если их нарисовать или мысленно там разместить). И помогают идеально верно начать чертить угловые три квадрата по отношению к центральной композиции.

Прибегнув к этой технике, вы очень быстро и без ошибок начертите всю схему. Потом начертите две окружности, расположив их на примерно таком же расстоянии друг от друга, как и на оригинале.

Теперь наступает этап подгонки чертежа под идеальную геометрию. На этом этапе имеется также ряд подсказок для неискушенного чертежника. По внешней окружности имеется множество явных точек. Они совершенно точно, что-то значат. Что именно, вы понимаете, когда начинаете, желая узнать все пересечения рисунка, проводить линии, используя центры квадратов как ориентиры.

Вообще весь чертеж создается как бы без заранее расчерченной поверхности. Его точки и части самодостаточны в создании идеального геометрического рисунка на параллельно создаваемой поверхности с ориентирами. Надеюсь, вы поняли, что я сказал.

Заранее отстраняясь от оригинала и разместив точки (по четыре) в каждом квадрате по центру треугольника, составляющего каждый малый квадрат, получаем ориентиры для проведения линий. Причем линии, проведенные в четырех плоскостях (на крест прямо и под углом), идеально параллельны друг другу, – и те, которые ориентированы на центры квадратов и те, которые ориентированы на точки в центрах треугольников. Из них же и составляется внешний квадрат своими линиями проходящий по центрам внешних треугольников большого внутреннего квадрата.

Не правда ли любопытные результаты для древнего геоглифа?!

Теперь мы отчетливо замечаем, что, несмотря на кажущееся количество точек по внешнему кругу, то десять, то шесть, в участках между внешними группами угловых трех квадратов, их на самом деле по девять. Именно такое количество пересечений выходит у окружности с ориентированными на правильное геометрическое соотношение линиями. Центральная “звезда” также ориентирована (но только некоторыми своими линиями) на параллели уже созданные нами на основе взаимного соотношения и правил начертания, геометрии.

Окружность рядом со “звездой” левее, скорее всего, имеет вспомогательное значение и указывает что-то вроде угла поправки и т. п. от чего-то основного, например, системы координат.

Итак создав, прошу обратить внимание, на основе взаимных соотношений без заранее расчерченной поверхности первый вариант чертежа, замечаем вывод первый.

Все в нем гармонично указывает друг на друга и помогает не только начертить рисунок идеально и по правилам, но и создает некую систему координат для любого идеального чертежа. То есть, если из созданной системы стереть наш рисунок, то останется правильно расчерченная система для создания любого другого рисунка по правилам геометрии.

Тут же замечаем, что, если, например, чертить это все на земле неким лазером, то надо зависнуть в воздухе над точкой центра рисунка метрах в ста над поверхностью, а то и выше, и, наложив координатную сетку, приступить к начертанию то ли посредством создания точек, потом соединяемых на земле, то ли сразу всего, это уже кто на что горазд. Задаче нынче вполне выполнимая, но попрошу заранее учесть стоимость этого баловства и, исходя из этого, его смысл.

Вывод второй. Возможно, это пособие по созданию геометрической координатной системы.

Исходя из правил геометрии и идеальности начертания, мы получаем по девять точек пересечения в четырех местах внешней окружности, всего 36 точек. Восемьдесят точек внутри квадратов и по пять точек четыре раза в местах, где внешняя окружность пересекается с угловыми группами квадратов = 20 точек. Всего 56 точек на внешней окружности и 80 внутри квадратов = 136 точек всего.

Но это основных точек! Если нам понадобится уменьшить системную сетку, то мы можем на равных расстояниях между параллельными линиями провести еще линии и точек получится практически астрономическое количество.

Вывод третий. Исходя из этого можно с уверенностью заключить, что видимые точки – не что иное как только ориентиры для правильного чертежа, но не как не что-то еще несущее, например, скрытые данные в числах. Особенно в этом доказательстве помогает наличие четырех точек, стоящих отдельно от всех на местах пересечения “невидимых” квадратов между группами внешних угловых и внутренних квадратов.

Но не будем забывать о том, что мы искусственно изменили чертеж, подогнав его под правила идеальной геометрии. Сделали мы это, во-первых, потому, что знаем эти правила заранее, ну и в виде маленького эксперимента. А теперь попробуем сделать тоже самое, но рисунок оставим, как он есть. Изменения коснутся в первую очередь точек внутри групп квадратов. Во внутренней группе точки расположены почти на линии стороны, а на внешних группах квадратов они смещены почти в точку пересечения, к центру квадрата.

Что же выйдет у нас, если мы попытаемся все это перечертить по этой схеме, то есть по тому, что мы и видим на плато “Пальпа”.

Проводя параллельные прямые, ориентированные на точки внутри малых квадратов, мы заметим, что теперь параллельные прямые находятся не на равных расстояниях друг от друга; еще мы заметим, что, проходя через центральную “звезду”, эти прямые пересекают ее без учета параллельности каких-либо линий рисунка. Исходя из проведенных по этим точкам линий, невозможно выстроить правильный рисунок и вычертить второй большой квадрат. Да, в общем, ничего толком нельзя сделать, исходя из этих линий. А если наложить правильный чертеж и тот, что есть на самом деле со всеми линиями, которые мы проводили по точкам, то получится просто хаотичное пересечение линий. Спрашивается, а зачем они тогда нужны?!

Но вспомним, что мы построили геометрически правильный чертеж, лишь изменив реальный рисунок, так сказать, исправив его. Так что же: первоначальный чертеж – пособие? Но тогда оно неправильное. Учить надо последовательно, не задавая сходу задач с неправильными условиями. Из них невозможно вывести единственно верное решение.

Представить себе, что тот, кто это все делал, просто ошибся сам, или не имел достаточных средств для точного исполнения, намекая подсказками на правила геометрии (везде и всегда единые), теоретически можно. Знания есть, нет точных инструментов, и вот он исполнил, но не идеально, а чтоб догадались, оставил подсказки. Тогда все равно, что это такое? Просто привет из прошлого, говорящий, что, мол, неверно вы, ребята, историю свою знаете; были очень давно уже те, кто правила всякие постиг, подумайте, мол, об этом. Слишком просто. Зашифрованная информация? Может быть, но выловить в этих соотношениях смысл – все равно, что сосчитать все звезды на небе. Цифр так много, и самое главное, что они могут меняться в зависимости от того, как вы что нарисуете, а это уже не точные указания.

Но вот предположения о том, что это может быть некая система координат, вполне живуче.

Тогда мы видим некий намек на нашу систему, построенную на идеальной геометрии и систему нам незнакомую, выстроенную на тех точках-ориентирах, которые и нарисованы. Накладываясь друг на друга, эти “сетки”, вполне возможно, дают какое-то соотношение, призванное нечто нам поведать. Линия с окружностями в стороне также, наверняка, подсказывает, что-то дополнительно об этом же.

Весь вопрос в том, где применимы эти системы координат, на поверхности или в небе.

Если на поверхности, то на чьей? Одна на нашей, другая на той, откуда создатели рисунка? Тогда это нужная, дружественная информация. Только вот где искать эту поверхность – не понятно, космос велик, да и Земля нам пока не мала.

В общем, тут найдется место и для приверженцев Атлантической теории и для сторонников пришельцев.

Неправильная “сетка” может быть и поверхностью Атлантиды и указателем в звездном небе, просто другой системой координат, неверно исполненным правильным вариантом, специально запутывающим вариантом для тех, кто не использует правильной геометрии. Очень много вариантов, и все они жизнеспособны.

Лично мне более всего по душе вариант, что это – некий ориентир на дороге, и пытаться его расшифровать, конечно, можно и нужно, но шансов мало. Дорожный знак. В нем указаны поправки курса для дальнейшего следования, и одновременно он сам свидетельствует, что данное местоположение какое-то вот такое, и никакое другое. Пролетая мимо, экспедиция корректирует траекторию или убеждается, что она верна итак.

Честно говоря, может быть, его надо и стереть, от греха подальше. Кто там по этим знакам летал, бог его знает. Прилетят потом (для световых скоростей, например, их минуты – наши столетия), убедятся, что курс правильный. Ба, а тут муравьи какие-то расплодились за это время, и давай их травить и изучать. Психология-то разная, наверняка: что нам дорого и свято, им – тьфу просто, ерунда, какая-то. Вы, например, долго горюете за убитым вами тараканом? А задумываетесь ли вы, инстинктивно и без малейших сожалений убивая его? А на каком таком основании мы все решили, что вот этот таракан не имеет право пробежать по полу? На основании права сильнейшего, и не отрицайте, что это – не так. Если вы не согласны, это значит, что вы даже не способны себе отчет правильный в своих же действиях отдать. Что уж говорить о правильных выводах и поступках.

Так вот, изучить, зарисовать, измерить и стереть поскорей, к чертовой матери. Нечем там любоваться, долюбуемся, поздно будет.