После прочтения статьи А.Склярова “Компьютер Древнего Китая” захотелось попробовать свои силы в поиске закономерности расположения номеров гексаграмм в таблице Книги Перемен.

Задачу можно сформулировать так: определить закономерность – значит определить, почему в ячейке с координатой XY стоит номер именно этой гексаграммы. Или почему гексаграмме в ячейке XY присвоен именно этот номер.

В процессе попытки найти закономерность пришла идея подойти к решению задачи с точки зрения нумерологии. Известно, что нумерология приписывает цифрам и числам определенные свойства. Соответственно значение и смысл любого события выражаются через свойства цифр и чисел, связанных с этим событием. Причем значение имеют не только сами цифры, но и порядок их следования в числе, состоящем из них. Скажем, цифра 9, полученная из числа 63 как 6+3, отличается по свойствам от полученной из числа 72 как 7+2.

Каждая гексаграмма имеет код (число), определяемый координатами ее ячейки XY (код определяется по методу из статьи А.Склярова). Этот код определяет нумерологическое значение гексаграммы. Нумерация же гексаграмм определяет ход развития событий путем установления последовательности изменения нумерологических значений гексаграмм. В этом случае расстановка номеров гексаграмм в таблице Книги Перемен дает нам в общем виде ход развития событий в той последовательности, в какой ее определил составитель, исходя из своего мировоззрения.

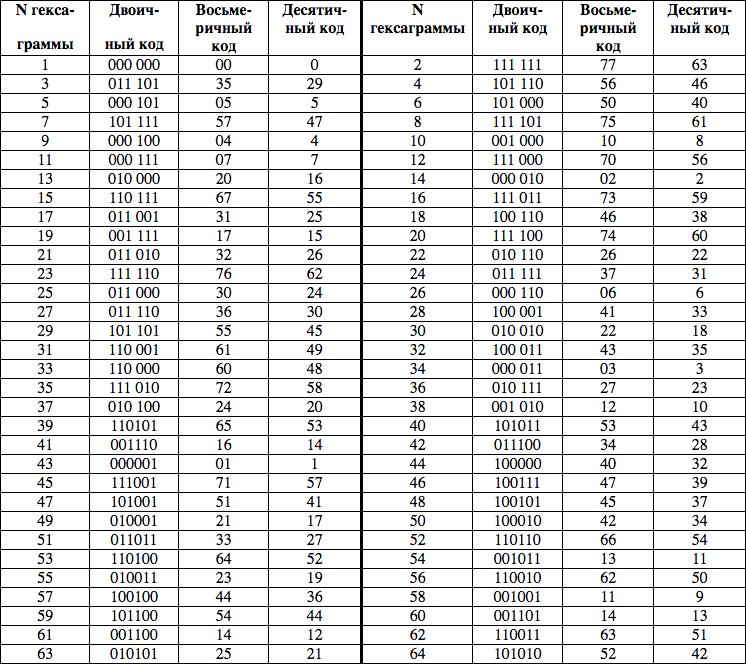
Причем, возможно, что нечетные номера задают ход развития инь, а четные ян (или наоборот). Т.е. можно рассматривать две последовательности нумерологических кодов: нечетная 0-29-5-47-4-7… и четная 63-46-40-61-8… На эту мысль наводит то, что пары гексаграмм образуются путем встречного прочтения, что может символизировать борьбу противоположностей (инь и ян), единство же их в том, что таким способом образования они однозначно связаны друг с другом и образуют пару.

Для проверки гипотезы нужно определить нумерологические значения кодов для каждой гексаграммы (по правилам китайской нумерологии) и сравнить с теми толкованиями, которые дает Книга Перемен. Возможно, они совпадут! Причем, следует ожидать, что это значение будет как бы зеркальным для пары номеров. Вполне возможно, что при нумерологических вычислениях нужно брать значения кодов и проводить вычисления в восьмеричной системе счисления, т.к. координаты ячеек меняются от 0 до 7, и использование восьмеричных чисел кажется более естественным. Номер же гексаграммы можно брать в любой системе счисления, т.к. он задает только порядок их следования. К сожалению, мои познания в нумерологии не позволяют провести такую проверку. Может, специалисты в этой области захотят попробовать свои силы?

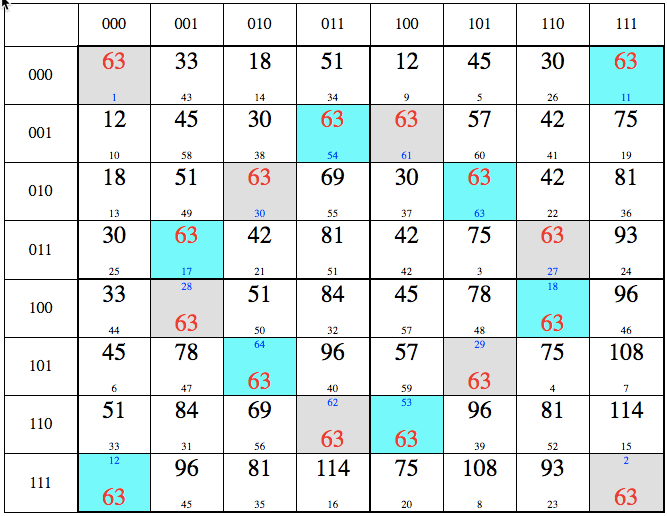
В качестве небольшого эксперимента я взял коды для каждой пары гексаграмм и сложил их, затем сложил цифры получившихся чисел. Т.е. для пары гексаграмм 3-4 получим 29+46=75=>7+5=12=>1+2=3 и т.д.

Далее в таблицу гексаграмм для каждой пары вместо номера гексаграммы подставил получившуюся сумму. И вот что получилось (см. Таблицы 1, 2).

Таблица 1

В таблице 1 мелким шрифтом показаны номера гексаграмм, крупным – сумма кодов соответствующих пар гексаграмм. Серым цветом выделены пары гексаграмм, образованные путем инвертирования их кодов, т.е. замены в двоичном коде 1 на 0 и наоборот.

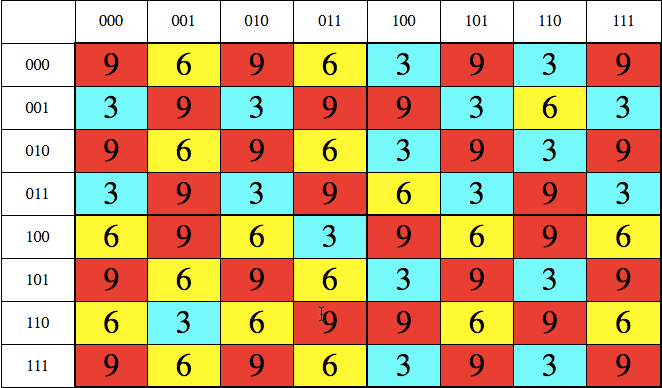
Таблица 2

Что интересно, в таблице 2 сумма цифр в любом ряду или столбце, а также по одной диагонали одинакова и равна 54, а 5+4=9. По другой диагонали выстроились одни девятки. Кроме того, большой квадрат разбивается на четыре меньших с диагоналями из троек, шестерок и девяток.

К сожалению, эти таблицы не связаны с порядком расположения номеров гексаграмм, а получаются лишь благодаря способу, которым образуются пары гексаграмм (обратное прочтение и инвертирование), т.к. при их построении числовое значение номера гексаграммы не использовалось. Т.е., если расставить номера гексаграмм в другом порядке, при сохранении способа образования их пар, то эти таблицы не изменятся.