Глава 1. Информативные и семантические признаки композиции
[one_half]Выделим основные составляющие композиции:
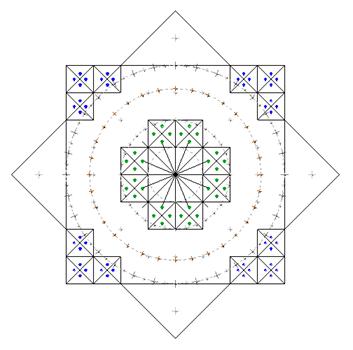
- Собственно сама восьмиконечная звезда, образуемая двумя квадратами: основной 8х8 и диагональный со стороной 12.
- Замаркированные ячейки маркировочными квадратами и перекрестиями диагоналей.
- Маркировочные точки. (или маркировочные квадраты, образуемые 4-мя точками, а в действительности круглыми ямями).
- 16-ти лучевая звезда в центре.
- Концентрические окружности. Окружности делятся последовательным делением на 2. Большая заметно делится на 32 части большими точками, а затем каждый сегмент еще на двое точкой поменьше, итого – 64
Прежде всего, нужно заметить, что мы имеем восьмиконечную звезду, отличающуюся от “правильной” восьмиконечной звезды, тем что состоит она из разных по размеру квадратов, и это объясняется тем, что наша композиция строится по модульной прямоугольной сетке. Восьмиугольник, образуемый пересечением квадратов получается не равносторонний (Рис. 2.а).
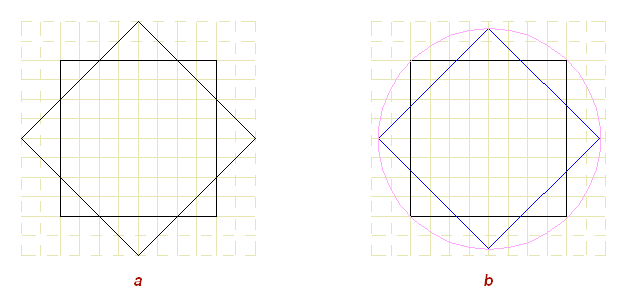
В правильной звезде (Рис. 2.b), построенной разворотом двух равновеликих квадратов, все уравновешено: отсекаемые треугольники равны между собой, в результате остается совершенно правильный восьмиугольник, имеет 16 осей симметрии повернутые на одинаковый угол относительно друг друга (360/16). Эти свойства приближают правильную звезду к окружности.
Иными словами, она обладает свойствами полярной или радиальной системы, где равновеликие величины равноудалены от центра.
[one_third]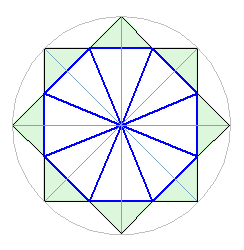
Но есть один недостаток: правильная звезда не укладывается в модульную сетку. Длина стороны восьмиугольника, как и длины сторон треугольников получаются иррациональными числами, основанными на бесконечном в дробной части числе sqrt(2). (иными словами ее трудно нарисовать на листочке в клеточку).
Это свойство отдаляет ее от квадрата, который является прямым полномочным представителем ортогональной системы. В модульной прямоугольной системе равные величины располагаются параллельно осям (а не по окружности, как в полярных системах).
Квадрат и равносторонний треугольник – две правильные фигуры, которые способны делиться на себе подобные без остатка. Т.е. площадь этих фигур заполняется полностью подобными им фигурами кратными им по размеру. Что придает этим фигурам важное свойство – модульность, определяющее параметры их внутреннего пространства. Каждая составляющая такой системы может быть самостоятельной подобной системой.
[/two_third_last] [one_third]
Но вернемся к узорам.
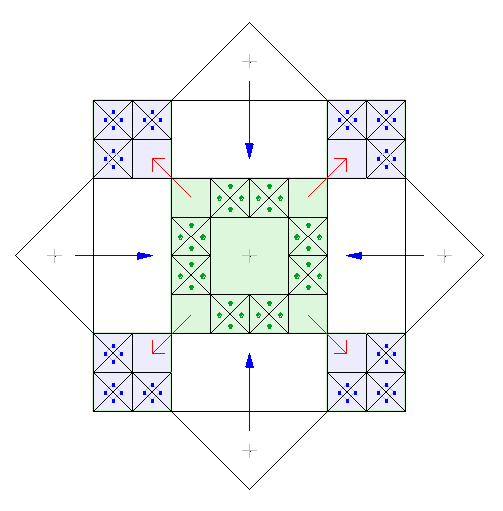
Из центра композиции на геоглифе расходятся 16 лучей. Восемь направлений (ортогональные и диагональные) совпадают с модульной сеткой.
[/two_third_last]С остальными – проблема. Возможны два варианта:
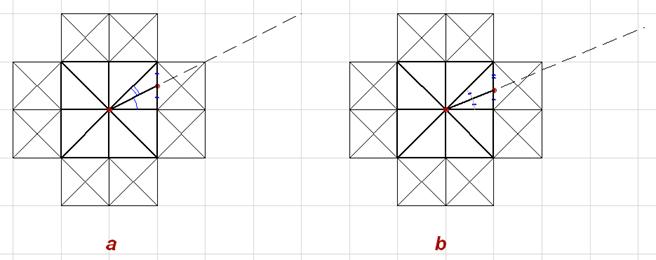
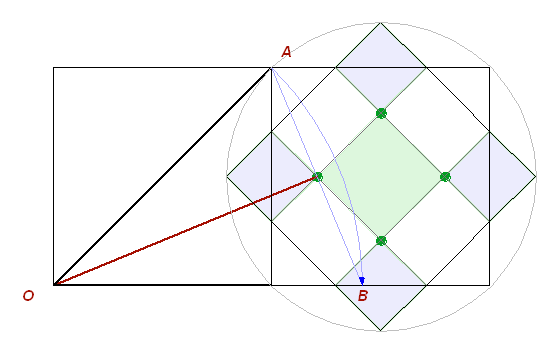
a) подчиниться правилу ортогональной системы и разделить пополам сторону ячейки (вариант а, Рис. 5);
b) либо по правилу правильной звезды разделить пополам угол (вариант b, Рис. 5):
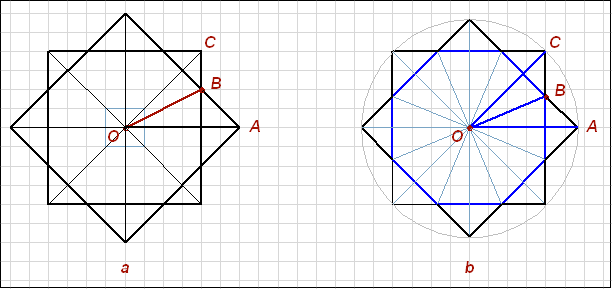
В первом случае мы следуем правилу общей композиции, но сталкиваемся с ее недостатком: угол AOB не равен углу BOC.
Во втором случае, мы получаем 16 лучей равномерно распределенных по окружности, но теряем равномерное деление сторон квадрата.
(то же, но увеличим центральную часть)
При неточности скального рисунка (а там погрешности в этом масштабе около 1-2 толщины линии), было бы трудно отличить какой именно вариант там используется. Лучевая звезда в разных вариантах выглядела бы почти одинаково.
Но об этом позаботились. На геоглифе точки через которые проходит луч обозначили:
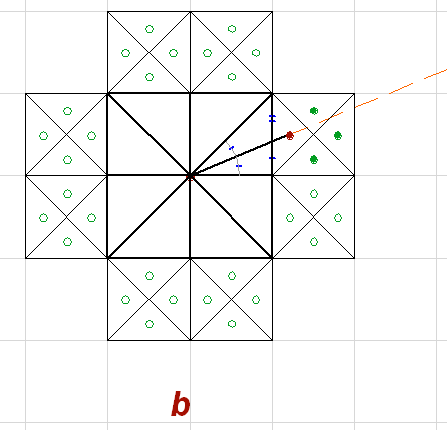
Точка лежит на середине высоты ячейки, но сдвинута от вертикальной стороны.
Только в этой точке биссектриса угла пересечет горизонтальную ось ячейки.
Именно деление угла на равные части используется при построении 16 лучей. Образуется угол правильного восьмиугольника, а в основе звезды лежит не правильный, “ортогональный” восьмиугольник. Это противоречит логике ортогонального модульного построения общей композиции, но проецирует ту же логику (деление на 2) на радиальную систему. Таким образом, в композицию добавляется полярная система.
Обнаруживается конфликт (в противопоставлении) двух различных геометрических систем : правильной восьмиугольной звезды, построенной по принципам полярной системы, и “неправильной”, построенной на ортогональной модульной основе.
Этот конфликт заставляет систему модифицировать структуру внутренних связей, в стремлении к равновесию.
А вот для чего тогда остальные три точки?
Формируя собой диагонально повернутый квадрат, они показывают, что точки лежат именно на серединных осях ячейки, а не где-то ближе или дальше к вершине. И диагональные перекрестия ячеек, тоже помогают воспринять неточный рисунок правильно.
То есть, маркировка в (этом случае) нанесена для того, чтобы указать на то, что именно угол делится пополам лучами, а не сторона ячейки, как можно было бы, следуя логике общей композиции, предположить.
В противном случае, построив биссектрисы достаточно было бы остановить луч на стороне квадрата, в крайнем случае, довести до первой точки. Но нам даются именно все четыре точки, которые ассоциативно связывается в квадрат и с его помощью хорошо прочитываются правила построения.
Маркировочные точки, получается, нанесены не случайно, и не из эстетических соображений, а как уточнение чертежа, дающее гарантию прочесть чертеж правильно.
Почти одинаковая величина углов, получаемых в разных вариантах, может внести ошибку при прочтении, и, с расчетом того, что изменение логики построения может оказаться не замеченным, на этом моменте акцентируется внимание. Точки активно показывают, подчеркивают, что именно правила “правильной восьмиконечной звезды” работают в этой части чертежа. А это говорит о том, что чертеж обладает свойствами иллюстрации, т.е. он нарисован с учетом того что его будут читать. Маркировка, как семантические элементы, используется в качестве пояснений к чертежу, но для кого предназначены эти пояснения? И почему так важно одинаковые там углы или нет? Единственной ли является “проблема построения лучей”, или чертеж содержит гораздо больше информации?
Выводы об иллюстративном, указательном характере маркировки подтверждаются и следующим.
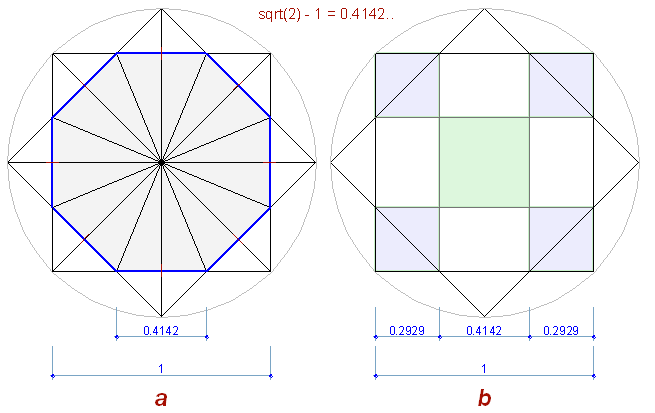
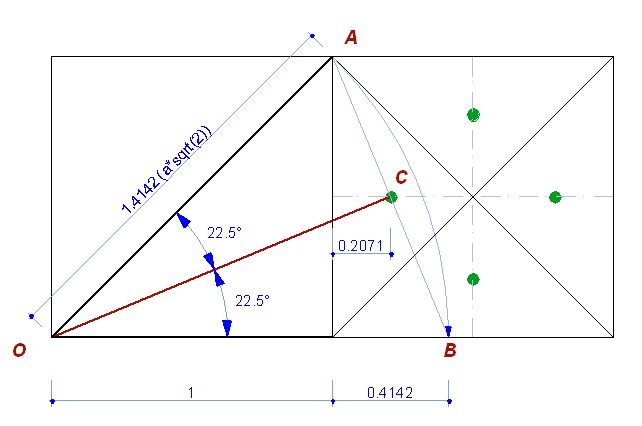
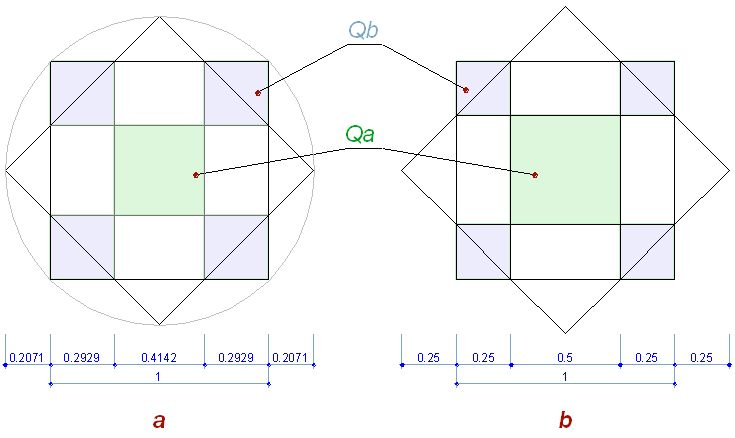
При пересечении, два повернутых квадрата образуют правильный восьмиугольник (Рис. 9.a), со стороной равной sqrt(2) – 1 (при стороне квадрата = 1). Правильный восьмиугольник основан на пропорциональных отношениях стороны квадрата к его гипотенузе, выражающееся через корень квадратный из 2. И деление квадрата (Рис. 9.b) вершинами восьмиугольника происходит тоже с таким же пропорциональным коэффициентом, на иррациональные части.
Повернув этот рисунок (Рис. 9.b) на 45°, увидим, что это и есть маркировочные квадраты, обозначенные точками на геоглифе:
Точки геоглифа в ячейках соответствуют иррациональным ячейкам квадрата правильного восьмиугольника.
Остается догадаться – где используются меньшие (синие) квадраты?.
20 из 64-х ячеек основного квадрата “замаркированы”.
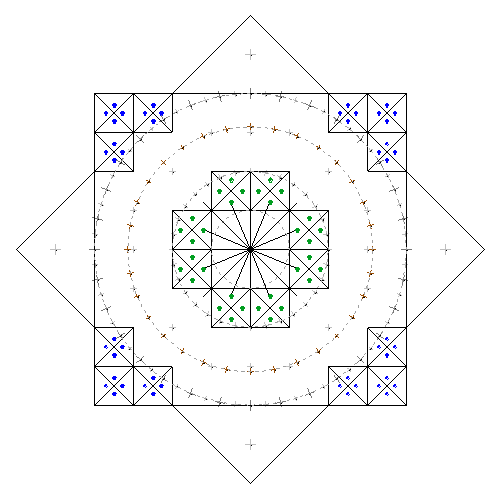
На снимках геоглифа хорошо заметно, что размеры маркировочных квадратов различаются. Ячейки основного квадрата, расположенные в углах (12 шт.), маркируются явно меньшими по размеру квадратиками (я обозначил их синими точками), чем ячейки расположенные вблизи центра (8 шт. – зеленые точки). (Основной квадрат 8х8, а диагональ повернутого квадрата – 12)
Назовем их для удобства Qа – больший, и Qb – меньший:
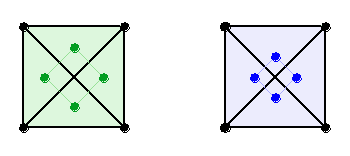
Таким образом ячейки делятся на четыре типа: сначала на пустые и замаркированные, затем замаркированные большим квадратом Qа и малым Qb.
Если мы наложим пропорциональную матрицу, полученную на Рис. 9.b то заметим, что схема маркировки ячеек Qа и Qb квадратами совпадает с расположением соответствующих квадратов матрицы:
В неправильной звезде пропорции матрицы адаптируются к модульным отношениям:
И так мы видим, что матрица Qa–Qb квадратов (Рис. 14), включена в композицию как система пропорциональных отношений правильного восьмиугольника для построения 16-ти лучей, и выступает еще в качестве схемы маркировки ячеек, связывая прямоугольную и полярную систему. Расположение замаркированных ячеек еще раз подводит нас к тому, речь идет об отношениях полярной и ортогональной системы.
Что получается? Из центра звезды берет начало геометрия радиальной системы, а в результате нарисована прямоугольная звезда, подчиненная правилам ортогональной модульности.
Нарисовать уточек в углах, а по середине лодочку – это еще можно понять. Но рисовать квадратик со стороной относящейся к стороне ячейки в пропорциях построения радиальной системы и наслаждаться радостью того, как он выглядит, распределяя его по кругу в прямоугольной системе в виде замысловатых точек – это уже сложнее отнести к развлечению.
Получается, что расположение помеченных ячеек, размеры маркировочных квадратов являются явно демонстрируемыми признаками включения в общую композицию, построенную на модульной ортогональной основе, элементов радиальной системы правильной восьмиконечной звезды. Намекают на близость этих систем и на отличия, которые в корне меняют внутренние свойства композиции. Наличие таких внутренних связей между элементами, убеждает меня в том, что геоглиф носит информативный характер.
Технология элементов-подсказок, включенных в общую схему и так гармонично в ней работающих, исполняя функцию указательных знаков – не очень типична для традиционных методов изложения информации, берущих свое начало от математиков-философов древнего мира. Эстетическая составляющая является лишь канвой, основой для изложения информации, подобно игре слов в поэтическом изложении, несущей послойно уложенный глубинный смысл, явно не проявляющийся в конкретных словах. Л. Кэролу возможно доставляло удовольствие упаковывать математические измышления в забавные стихотворения для маленькой девочки. Но он имел образование соответствующее.
Каждый включаемый элемент в композицию, является значимым носителем некоторой информации, своего рода символом некоторого геометрического языка.
И мы рассмотрели только иллюстративный, демонстрационный характер композиции.














Очень похоже на настроечную таблицу.