Матрично-тензорная интерпретация таблиц древнекитайской “книги перемен” и генетического кода

Настоящая публикация посвящена дальнейшему выявлению структурных параллелизмов между системами генетического кода и древнекитайской “Книги перемен”. Она является продолжением авторских публикаций на эту тему [11-16].

“Книге перемен” (другие ее названия – “И цзин”, “Канон перемен”, “Чжоу и”, “Циклические перемены”) посвящена огромная научная и околонаучная литература. Приведем три характерные цитаты о ней из монографии [18, с. 3, 8, 10, вступительное слово Кобзева]:

“”Канон перемен” относится к числу величайших и одновременно наиболее загадочных творений человека. С точки зрения породившей его китайской культуры (древнейшей из ныне продолжающих свое существование на земле) он представляет собой нечто еще более значительное – творение Сверхчеловека, запечатлевшего в особых символах и знаках тайну мироздания. Поэтому “Канон перемен” требует к себе особого отношения – как к книге книг, священному писанию, одному из духовных чудес света”. “Такой же, как Библия для западной культуры, книгой книг китайской культуры является … “Чжоу и”. Библия и “Чжоу и” сходны и по своей роли духовного центра соответствующих культур, и по степени загадочности происхождения и глубинного смысла, продолжающей сохраняться, несмотря на многовековые подвижнические усилия их исследователей”. “”Чжоу и” – наиболее авторитетное произведение китайской канонической и философской литературы,… оказавшее фундаментальное парадигматическое воздействие на всю культуру традиционного Китая и сопредельных стран. Выраженные в нем идеи… создали своеобразное мировозрение и методологию, оказали огромное влияние на развитие философии, религии, естественных наук, литературы и искусства в древнем Китае, в результате чего китайская культура стала совершенно уникальной в истории мировой культуры и внесла свой вклад в человеческую цивилизацию. Символы и принципы “Чжоу и” пронизывали буквально все сферы жизни традиционного Китая – от теоретических эмпиреев и высокого искусства до бытовых предметов и украшений. Из этого же источника черпали астрономы и астрологи, навигаторы и гадатели, музыканты и врачи, историки и администраторы, мастера боевых искусств и знатоки тайн продления жизни”.

“”И цзин” – книга, которую мудрецы и ученые всех поколений полагали ключом к разгадке таинств Природы и неисчерпаемой сокровищницей метафизической премудрости, объясняющей все явления Вселенной” [5, с.92].

Многие западные естествоиспытатели не раз обращались к “Книге перемен”. Так, основатель “аналитической психологии” Карл Густав Юнг построил в связи с ней учение о коллективном бессознательном. Согласно Юнгу, рассматриваемые в ней триграммы и гексаграммы (гуа) “фиксируют общечеловеческий набор архетипов (врожденных психических структур)” [18, с. 12]. Нильс Бор выбрал символ инь-ян своим гербом. Многие современные физики, ощущающие единство окружающего мира, так или иначе, связывают свои теории с объединяющими всю природу идеями древневосточной культуры. Это нашло отражение, например, в “восьмеричном пути” Гелл-Манна и Неемана (Gell-Mann, Ne’eman, 1964), бинарной геометрофизике (Кулаков, Владимиров, Карнахов, 1992) и др.

Значительный интерес к системе инь-ян проявляет современная лингвистика, в которой развиваются теории бинарных оппозиций как унифицирующей основы различных языков (Якобсон, 1985; Иванов Вяч.Всев., 1999, и др.). “Книге перемен” в связи с различными вариантами возможных конкретных приложений ее конструкций посвящены труды многих философов, искусствоведов, историков, представителей других областей науки (Бахтияров К.И., Виногродский Б.Б., Григорьева Т.П., Еремеев В.Е., Идлис Г.М., Кобзев А.И., Лукьянов А.Е. и др.). Молекулярная генетика тоже не обошла вниманием “Книгу перемен” [11-16, 22] . Значительное внимание современной науки к древневосточным концепциям, на которых, в частности, базируется эффективная и самобытная восточная медицина, акцентировано в содержательной книге Е.Н.Князевой и С.П. Курдюмова [7]. Она посвящена проблемам самоорганизации и ставит в этой области задачи синтеза западного математического естествознания и древневосточных учений, обогащенных тысячелетними практиками и наблюдениями. Краткий обзор современных монографий, журналов и исследовательских обществ по изучению “Книги перемен” в восточных и западных странах дан Кобзевым во введении к книге [8]. Этой же проблематике посвящено большое число сайтов в Интернете. Группы по изучению “Книги перемен” имеются во многих не только восточных, но и западных университетах, например, Принстонском, Московском физико-техническом институте и др.

Влияние названной Книги широко представлено в современной жизни стран Востока. Так, государственный флаг Южной Кореи несет на себе символы триграмм Работает огромное число специализированных школ, в которых наставники передают учащимся методологические аспекты практического применения древних знаний в русле “И цзин” к самым различным практическим проблемам: от совершенствования духа и тела до организации жилья и офисов, прогнозирования событий и пр. Одним из характерных современных примеров может служить применение “Книги перемен” на Тайване для обеспечения авиационной безопасности, представленное в Интернете на сайте “”И цзин” и безопасность авиаполетов”: http://w3.one.net/~linch9/iching_flight_safety.htm (ред. – ссылка не работает).

Авторами обнаружен целый ряд структурных параллелизмов между системами “Книги перемен” и общебиологическими системами генетического кода. Это стало возможным в результате матричного представления и анализа множества элементов генетического кода, в том числе использования тензорного произведения матриц [11-16, 22]. Применение аналогичного матричного анализа к системам “Книги перемен” позволило получить новые результаты о специфике этих систем, к изложению которых мы и приступим.

Главной таблицей в “Книге перемен” является знаменитая таблица 64 гексаграмм в порядке Фу-си (Рис. 1), которая считалась всеобщим природным архетипом. Гексаграммы представляют собой укладку из шести черт двух типов: прерывистых, символизирующих Инь (женское начало), и непрерывных, символизирующих Ян (мужское начало). Каждая черта гексаграммы имеет индивидуальный номер. Единая нумерация шести черт вертикальной гексаграммы идет последовательно снизу вверх однонаправлено с ростом растений, т.е. нижняя черта имеет номер 1, а верхняя – номер 6. Наряду с гексаграммами рассматриваются также диграммы (укладки из двух черт) и триграммы (укладки из трех черт), в которых нумерация черт также идет по возрастающей снизу вверх. “Триграммы, гексаграммы и их компоненты во всех комбинаторно возможных сочетаниях образуют универсальную иерархию классификационных схем, в наглядных образах охватывающую любые аспекты действительности – части пространства, отрезки времени, природные стихии, числа, цвета, органы тела, социальные и семейные положения и т.д.” [18, с.10].

Рис.1. Квадратное расположение гексаграмм по Фу-си из “Книги перемен”, дополненное указанием для каждой гексаграммы ее двоично-числового аналога и его эквивалента в десятичной системе счисления.

Именно это расположение гексаграмм поразило и воодушевило в свое время Лейбница при разработке им основ двоичной системы счисления и идей формализации мыслей человека за счет создания некоторого общего языка, символы и слова которого должны направлять наш разум. Лейбниц увидел, что, если каждую гексаграмму представить как шестиразрядное двоичное число, заменив каждую ее прерывистую черту цифрой “0”, а каждую непрерывную черту – цифрой “1”, а затем прочитать полученные двоичные числа в десятичной системе счисления, то древняя последовательность 64 гексаграмм по Фу-си в точности совпадет с порядковым рядом десятичных чисел от 0 до 63. Аналогично для расположения 8 триграмм по Фу-си получается в двоичном коде порядковый ряд от 0 до 7. “Лейбниц усмотрел в этом подобии … свидетельство предустановленной гармонии и единства божьего промысла для всех времен и народов” [18, с. 12].

Каждая гексаграмма по древнекитайской традиции рассматривается как состоящая из двух самостоятельных триграмм – нижней и верхней. Вот как написано об этом в книге [18, с.86-87]: “”В теории “Книги перемен” принято считать, что нижняя триграмма относится к внутренней жизни, к наступающему, к созидаемому, а верхняя – к внешнему миру, к отступающему, к разрушающемуся.… В верхней и в нижней триграмме аналогичные позиции имеют ближайшее отношение друг к другу. Так, первая позиция стоит в отношении аналогии к четвертой, вторая – к пятой и третья – к шестой… Если соотносительные позиции (1-4, 2-5, 3-6) заняты различными чертами, то считается, что между ними “есть соответствие”; в случае однородности черт на соотносительных позициях между ними “соответствия нет””.

С точки зрения опыта построения октетной матрицы 64 генетических триплетов, которая оказалась идентичной древнекитайской таблице 64 гексаграмм, эту таблицу следует понимать следующим образом. В таблице 64 гексаграмм речь идет о 64 объектах, каждый из которых состоит из трех упорядоченных частей (типа триплетов генетического кода). При этом каждая из этих трех частей в свою очередь наделена парой бинарных (инь-ян) признаков; для записи бинарного признака одного вида для каждого из этих трехчастных объектов используется только нижняя триграмма гексаграммы, а для записи бинарного признака второго вида – только ее верхняя триграмма. В результате оба вида признаков для каждой из трех частей такого объекта представлены на соотносительных позициях 1-4, 2-5, 3-6 соответствующей ему гексаграммы. Эта особенность древнекитайской матрицы с размером (8х8) будет учтена ниже при установлении ее скрытых связей с другими структурами “Книги перемен” и при ее формальном выводе из простейшей базовой матрицы с размером (2х2).

Базовое значение в “Книге перемен” имеет четверка диграмм (см., например, [18]):

Из этой четверки диграмм авторы построили базовую матрицу S с размером (2х2), исходя из аналогии с матрицей четырехбуквенного генетического алфавита C, A, U, G:

Оказывается, что при возведении этой базовой матрицы S в третью тензорную (кронекерову) степень порождается матрица 64 гексаграмм по Фу-си, если при построении результата тензорного умножения матриц учитывать только что сказанное о значимости соотносительных позиций 1-4, 2-5, 3-6 в гексаграммах. Речь идет о том, что в диграммах, тетраграммах и гексаграммах следует четко различать верхнюю и нижнюю половины и при тензорном перемножении матриц черты из верхней (нижней) половины исходной полиграммы размещать только в верхней (нижней) половине итоговой полиграммы на соответствующей позиции. В остальном следует выполнять классическую процедуру тензорного перемножения матриц, наглядно описанную, например, в книге [2, глава 10]. Это перемножение строится на приписывании сначала второй матрицы справа к каждому члену первой матрицы, выступающему тем самым в роли коэффициента при этой второй матрице, а затем к обычному умножению на этот коэффициент всех членов второй матрицы. В итоге получается матрица увеличенной размерности. Для получения древней матрицы 64 гексаграмм по Фу-си проще всего возвести в третью тензорную степень матрицу (2х2) из четырех букв (типа букв С, A, U, G), получив матрицу 64 триплетов из этих букв [12,1 4, 23], а затем заменяя каждый буквенный триплет гексаграммой из прерывных и непрерывных черт по следующему “китайскому” правилу. В каждом триплете заменяем каждую из четырех букв той диграммой из прерывных и непрерывных черт (инь и ян), которая соответствует ей в написанной выше матрице S; нижнюю черту каждой диграммы заносим в нижнюю триграмму гексаграммы, а ее верхнюю черту – в верхнюю триграмму, сохраняя естественный порядок очередности: черты той диграммы, которая соответствует первой букве триплета, ставим на соотносительные позиции 1-4 гексаграммы, черты диграммы второй буквы триплета – на соотносительные позиции 2-5, а черты диграммы третьей буквы триплета – на соотносительные позиции 3-6 гексаграммы. Этот тензорный алгоритм построения из матрицы 4 диграмм древнекитайской матрицы 64 гексаграмм соответствует точке зрения, изложенной в монографии [18, с. 101]: “Гексаграммы – это не триграммы, сплавленные воедино; это – две триграммы, расположенные по вертикали, одна над другой… Существуют изменения в гексаграмме от нижней триграммы к верхней, отсюда название И – “Перемены”, которые носит вся система”.

При анализе структур генетического кода содержательные результаты дало представление символьных матриц генетического кода в виде числовых матиц, получаемых заменой каждой буквы генетического алфавита (точнее каждого азотистого основания генетического кода) тем числом ее водородных связей, которые обеспечивают соединения комплементарных оснований в молекулах наследственности ДНК и РНК и которые давно подозревались многими исследователями на важную роль в передаче наследственной информации. У азотистых оснований A и U это число равно 2, а у С и G это число равно 3.

Интересно, что в Древнем Китае эти числа 2 и 3 служили основанием китайской арифметики и назывались числами Земли и Неба соответственно. Поэтому все те числовые свойства геноматриц, которые были получены авторами при изучении геноматриц в случае замены в них букв генетического алфавита на числа 2 и 3 водородных связей, воспроизводятся также на матрицах “Книги перемен”. В частности, оказывается, что эти древние матрицы имеют связь со знаменитым золотым сечением φ = (1+5^0.5)/2 = 1, 618… . Продемонстрируем это.

Известно, что четыре китайские диграммы молодых и старых Инь и Ян делятся на две подтипа. Один подтип включает в себя две диграммы, которые состоят из различных черт, называемых “соответственными”. Второй подтип включает в себя две другие диграммы с одинаковыми чертами в них (например, с двумя сплошными чертами), которые называются “не соответственными” [18, с.87]. Заменим в символьной матрице S диграммы с соответственными чертами числом 2, базовым для китайской арифметики, а диграммы с несоответственными чертами – также базовым числом 3. То же самое проделаем с китайской символьной матрицей 64 гексаграмм применительно к диграммам на соответственных позициях 1-4, 2-5, 3-6 (перемножая для каждой тройки таких диграмм заменяющие их числа 2 и 3 как это делается при тензорном перемножении матриц). В результате получим числовую матрицу S_Q и ее третью тензорную степень S_Q⁽³⁾ (числовой аналог матрицы 64 триплетов):

Эти матрицы тесно связаны с золотым сечением φ, что становится очевидным при извлечении из них квадратного корня, в результате которого образуются “золотые” матрицы, все компоненты которых равны только золотым сечениям в целой степени:

Матрицы S_Q⁽ⁿ⁾ с геометрической точки зрения являются метрическими тензорами, поскольку удовлетворяют условиям симметричности и невырожденности. Понятие метрического тензора является основным в римановой геометрии и ее обобщениях типа финслеровой геометрии. Из него выводятся тензоры кривизны, геодезические линии криволинейных пространств с внутренней метрикой и пр. Обнаружение связи матриц И цзин с золотым сечением и метрическими тензорами порождает новое направление мысли о сопряжении структур И цзина с идеями обобщенной кристаллографии. Напомним, что в современной обобщенной кристаллографии усиленно рассматриваются структуры, несущие на себе пропорции золотого сечения: квазикристаллы Шехтмана, мозаики Пенроуза, пентаграммы и пентасимметричные биологические тела, фуллерены, додекаэдры ансамблей водных молекул и пр. В ней также рассматриваются криволинейные структуры, описываемые римановой геометрией. Видимо, возможно углубленное понимание структур И цзина на базе идей обобщенной кристаллографии

Обратимся дополнительно к словам Щуцкого, ведущим к обнаружению других связей матриц И цзина с золотым сечением: “Особенное внимание уделяется при анализе гексаграммы второй и пятой позициям. Каждая из них является (в нижней или верхней триграмме) центральной, т.е. такой, в которой самым совершенным и уравновешенным образом выявляются качества триграммы.…” [18, с.87]. Рассмотрим числовую матрицу, соответствующую именно этим диграммам из черт 2 и 5 позиций в таблице 64 гексаграмм И цзин в предположении, что диграмма из однотипных черт заменяется числом 3, а диграмма из разнородных черт – числом 2:

Квадратный корень R из этой матрицы равен половине от золотой матрицы F(f), где f – золотое сечение 1, 618… . , т.е. R=0.5xF, где F =

Аналогичные результаты, но с несколько иным расположением тех же чисел в матрицах, мы получаем, рассматривая те же числовые эквиваленты диграмм на 1 и 4 позициях ( и на 3 и 6 позициях) гексаграмм И цзин.

По мнению авторов, древнекитайская “Книга перемен” оказала сильное влияние на Пифагора. Учение пифагорийцев о ключевой роли чисел в устройстве мира возникло не на пустом месте, а по многим данным развивалось в русле более древних восточных воззрений. Например, по китайским представлениям, четное число 2 являлось женским числом, а нечетное 3 – мужским числом. А вот как понимались эти же числа в школе Пифагора: “Целое число 2 рассматривалось как женское, которое не может породить новые тоны без участия мужского числа 3” [23]. Приведем другой пример о связи пифагорейского учения о гармонии с матрицами “Книги перемен”.

Матрицы S_Q⁽ⁿ⁾ могут называться квинтовыми, поскольку их структура демонстрирует квинтовые принципы организации, характеризуясь отношением музыкальной квинты 3:2 на различных уровнях: между суммами чисел в рядом расположенных по вертикали квадрантах, субквадрантах, субсубквадрантах и т.д., включая отношения квинты между соседними по величине числами в этих матрицах. Например, представленная матрица S_Q⁽³⁾ четыре вида чисел – 27, 18, 12, 8 – с отношениями квинты между ними: 27/18=18/12=12/8=3/2. Каждая квинтовая матрица S_Q⁽ⁿ⁾ содержит индивидуальную последовательность из (n+1) видов чисел в форме геометрической последовательности, коэффициент которой равен квинте 3/2. В семействе матриц S_Q⁽ⁿ⁾ , где n= 0, 1, 2, 3, …, реализуются следующие наборы чисел: 2, 3 (при n=1); 4, 6, 9 (n=2); 8, 12, 18, 27 (n=3); и т.д. (Матрицу при n=0 считаем состоящей из единицы и имеющей размер (1x)]). Выпишем эти наборы чисел из этого семейства матриц “Книги перемен” столбцами:

Оказывается, что числовой треугольник слева, выведенный нами из тензорного семейства матриц “Книги перемен” (и аналогичных матриц генетического кода), был известен уже около двух тысяч лет. Он опубликован математиком неопифагорийской школы Никомахом из Гераса в его известной книге “Введение в арифметику” как ключевой для учения о гармонии пропорций и теории музыки [22]. Об этом факте авторам сообщил американский математик Дж.Каппрафф (Jay Kappraff), написавший в личном письме, что его коллега Гари Адамсон (Gary Adamson), познакомившись с публикациями одного из авторов (С.В.Петухова) о семействе матриц генетического кода, открыл, что наборы чисел в них совпадают с числами треугольника Никомаха из Гераса. Справа от этого треугольника нами воспроизведен известный числовой треугольник Платона, называемый также тетрадой пифагорийцев. Видно, что его последовательности из чисел 2ⁿ и 3ⁿ совпадают с обрамляющими последовательностями треугольника Никомаха. Вероятно, последний был построен именно на тетраде пифагорийцев, которая использовалась ими, в частности, в качестве клятвы: “Клянусь именем тетрады, ниспосланной нашим душам; в ней источник и корни вечноцветущей природы”.

Отметим попутно, что замечательный поэт Велимир Хлебников, вероятно, под влиянием пифагорийских представлений о тетраде, состоящей из степеней чисел 2 и 3 (а значит, в конечном счете, под влиянием древнекитайских представлений “И цзин”), считал, что все состоит из двоек и троек [6, т.2]. Он писал, что 3ⁿдней – злое божество времени, “колесо смерти”, а 2ⁿ дней – доброе божество времени. И периоды истории он делил на хорошие периоды длины 2ⁿ и плохие – длины 3ⁿ . Это число 3ⁿ в матрицах S_Q⁽ⁿ⁾ “И цзин” занимает всю главную диагональ и только ее, а число 2ⁿ – вторую диагональ и только ее; вместе они образуют фигуру креста из матричных диагоналей. Эти матрицы имеют отношение к проблеме календарей и времени, но данные вопросы выходят за рамки статьи. В.Хлебников считал также, что весь мир есть стихотворение; соответственно таблицы Ицзин и генетического кода могут рассматриваться также как стихотворные формы.

Используя в качестве числовых аналогов пар молодых и старых Инь и Ян числа 6 и 9 (утроенные числа Земли и Неба), которые в Древнем Китае считались символами Инь и Ян, мы получаем из символьной таблицы 64 гексаграмм И цзин (и соответственно из символьной геноматрицы 64 триплетов) такую числовую матрицу, суммы чисел каждого столбца которой образуют последовательность чисел 144, 168, 168, 192, 168, 192, 192, 216 (эта матрица приведена в книге [11, с. 61]). Но эта последовательность, полученная нами из геноматриц и матриц И цзина, была известна уже в Древнем Китае под именем последовательности “счетных палочек” из древнего руководства “Числа превращений дикой сливы мэй-хуа” (русский перевод которой опубликован Б.Виногродским [1, c.269-292]), где она никак непосредственно не связана с матрицами И цзин.

Вообще, на базе оригинальных результатов анализа матриц генетического кода и “Книги перемен” авторами развивается культурологическое направление, условно именуемое ими “Геноарт” [13]. Оно включает создание тематически структурированных произведений графики, живописи, музыки, архитектуры, стихосложения, лингвистики и прочее. В частности, активно используется открытые авторами факты о том, что генетические последовательности молекул ДНК и белков несут на себе несколько закономерных вариантов натуральной генетической музыки. Она связана с пифагорейским музыкальным строем и выступает в роли языка согласования элементов системы генетического кодирования. Эти факты в настоящее время публикуются, а их практические приложения патентуются.

Оказывается, что психофизиологические феномены эстетики и гармонии пропорций структурно сопряжены с системой молекулярных параметров генетического кода и матрицами “Книги перемен”. В науке существует нерешенная проблема физиологических основ эстетики пропорций и музыки. Нобелевский лауреат по физике Р.Фейнман так охарактеризовал состояние этой проблемы, когда писал о неясных корнях чувства музыкальной гармонии: “Но далеко ли мы ушли от Пифагора в понимании того, почему только некоторые звуки приятны для слуха? Общая теория эстетики, по-видимому, ненамного продвинулась со времен Пифагора” [17, т.4, с.201]. Изложенные в этой статье материалы и другие результаты авторских исследований дают основания считать, что эстетические чувства и предпочтения имеют генетическую основу и структурно сопряжены с матрицами “И цзин”.

В виде небольшого отступления в область древнекитайской музыки и “Книги перемен” отметим музыкальное представление таблиц “Книги перемен” [15, 16], достигнутое авторами в ходе работ над аналогичными матрицами генетического кода. Оно тем более интересно, что история не сохранила древнекитайских музыкальных произведений. Эти произведения, согласно легендам, подчас демонстрировали высокую физиологическую активность, способность удивительно влиять на рост растений, лечить людей и пр. По мнению автора, в результате проводимых матричных исследований мы восстанавливаем знания об утраченных базовых музыкальных мелодиях Древнего Китая. Кроме того, мы получаем аргументы к новой точке зрения на возможное происхождение самих таблиц “Книги перемен”. Как уже отмечалось, музыка играла исключительную роль в жизни, культуре и идеологии Древнего Китая, в котором даже система мер и весов строилась в связи с музыкальными инструментами (см., например, [4, с. 76]). В свете этого можно полагать, что таблицы “Книги перемен”, прежде всего, таблица 64 гексаграмм в порядке Фу-си, построены как свод знаний о музыкальной гармонии, лежащей по представлениям китайцев в основе мироздания, в том числе, как запись квинтового музыкального строя. Данная точка зрения кажется достаточно естественной и снимающей пелену полной загадочности на происхождение таблиц “И Цзин”. В пользу этой выдвигаемой автором точки зрения на происхождение таблиц “И Цзин” можно привести ряд дополнительных аргументов. Так, числовое представление таблицы 64 гексаграмм “И Цзин” в виде матрицы S_Q⁽³⁾ получается при соответствующем алгоритмическом использовании чисел 2 и 3, которые традиционно назывались числами Земли и Неба соответственно и которые являлись основой древнекитайской арифметики. Но с точки зрения матриц “Книги перемен” существует прямое указание на связь основ музыки с Небом и Землей в классическом произведении “Весен и осеней” Люй Бувея в главе о музыке: “Истоки музыки – далеко в прошлом. Она возникает из меры и имеет корнем Великое единство. … Музыка покоится на соответствии между Небом и Землей” (данная цитата заимствована нами из книги [3, с.25], автор которой Г.Гессе является нобелевским лауреатом, знатоком и ценителем “И Цзина”).

Используя связь представленных выше квинтовых геноматриц с золотыми геноматрицами (или матрицами “И Цзин”), автор построил математический строй золотого вурфа (золотой вурф р = 0,5*f² = 1,309…), который близок к пифагорейскому строю, но вместе с тем заметно отличается от него (см. Рис. 2 и 3). Заполнение октавы (числовой интервал от 1 до 2) в случае пифагорейского строя задается, как известно, последовательностью 1, 9/8, 81/64, 4/3, 3/2, 27/16, 243/128, 2, а в случае строя золотого вурфа – последовательностью 1, p³/2, p⁶/4, р, p⁴/2, (1/p)*2, p², p⁵/2, 2. В обоих случаях имеет место диатоническая гамма и заполнение октавы посредством интервальных коэффициентов всего двух типов: тон-интервалов и полутон-интервалов. Для семиступенного пифагорейского строя тон-интервал имеет величину 9/8 = 1,1250…, а полутон-интервал – 256/243 = 1,0535.. . Для восьмиступенного строя золотого вурфа тон-интервал равен p³/2 = 1.1215…, а полутон-интервал – 4*р^-5 = 1.0407… .

Рис. 2. Последовательность интервальных коэффициентов в рассматриваемых математических строях.

Тон-интервал обозначен цифрой 1, а полутон-интервал – дробью ½.

Рис. 3. Частоты тонов в герцах и названия нот в семиступенном пифагорейском строе и в соответствующем восьмиступенном строе золотого вурфа для первой октавы.

Если полагать, что строй золотого вурфа (или, кратко, вурф-строй) имеет значение для музыкальной теории и создания на его основе музыкальных композиций повышенной физиологической активности (эти вопросы сейчас исследуются), то можно указанной последовательности его интервальных коэффициентов сопоставить последовательность тонов. Рис. 3 демонстрирует вариант такой последовательности тонов (нот) строя золотого вурфа. Этот вариант разработан, исходя из дополнительного условия, что совокупность частот его тонов содержит частоту 440 гц, которая соответствует ноте “ля” в пифагорейском строе и равномерно-темперированном строе и которая традиционно используется для настройки музыкальных инструментов (по некоторым литературным данным новорожденный издает первый крик на частоте ноты “ля”). Принимая во внимание минимальное различие между обоими строями, большинство нот строя золотого вурфа названо по аналогии с соответствующими и привычными всем названиями нот пифагорейского строя. Отличие заключается в добавлении буквы “м” в конце имени каждой ноты (например, “рем” вместо привычного “ре”), а также наличии дополнительной ноты под названием “пим”.

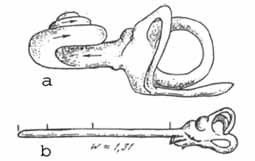
Следует отметить, что золотой вурф = φ²/2 известен в биоморфологии, как имеющий статус онтогенетического и филогенетического инварианта совокупных пропорций трехчленных кинематических блоков тела человека и многих животных [10]. Он был введен в книге [10] в связи с анализом неевклидовых симметрий в биологических телах. Понятие “вурф” играет важную роль в неевклидовой геометрии, а его перевод с немецкого языка означает “бросок”. Величина золотого вурфа имеет также отношение к акустическому восприятию: улитка человеческого уха состоит из трех завитков, отношения длин которых образуют геометрическую прогрессию с коэффициентом золотого сечения φ (Рис. 4). Двойное отношение длин таких трех отрезков равно золотому вурфу: p = φ²/2.

Рис. 4. Спиральная структура улитки человеческого уха (из книги [21]) с проективно-геометрической пропорцией золотого вурфа: а – спиральная улитка; в – улитка, развернутая в прямую линию с отношением длин ее трех завитков 1:φ: φ², дающих значение двойного отношения (вурфа) совокупной пропорции этих трех отрезков равное p = φ²/2.

Изложенное в статье позволяет лучше понять слова Конфуция: “Продлись мои лета, я бы пятьдесят из них отдал изучению “Книги перемен” [18, c.8].

Дополнительно отметим, что матрицы генетического кода и структурно родственные им матрицы “И цзин” естественным образом сопрягаются с идеями параллельных каналов передачи информации (см. данные о бинарных субалфавитах генетического кода и параллельных бинарных текстах в молекулах ДНК в публикациях авторов). Исследования этого направления позволили авторам обнаружить связь молекулярной системы генетического кода с матрицами Адамара и ортогональной системой функций Уолша, играющими важную роль в теориях кодирования, дискретных сигналов, квантовых компьютеров и др. На этой основе в настоящее время разрабатываются новые подходы к пониманию генетической системы и биологической самоорганизации (“ортогональная самоорганизация”), а также некоторых аспектов “И цзин” и роли спектрального анализа в устройстве и работе молекулярно-генетической системы.

Литература

1. Виногродский Б. Даосская алхимия бессмертия. М., София, 2003.
2. Газале З. Гномоны. От фараонов до фракталов. М., ИКИ, 2002.
3. Гессе Г. Игра в бисер. – Собрание сочинений в 4-х томах, том 4, Спб, Изд-во Северо-Запад, 1994.
4. Еремеев В.Е. Символы и числа “Книги перемен”. – М., Ладомир, 2005.
5. Ермаков М.Е. Китайская геомантия. Спб., Петербургское востоковедение, 1998.
6. Иванов Вяч. Всев. Избранные труды по семиотике и истории культуры. т.2, М., 2000.
7. Князева Е.Н., Курдюмов С.П. Законы эволюции и самоорганизации сложных систем. – М., Наука, 1994.
8. Кобзев А.И. Учение о символах и числах в китайской классической философии. М., Восточная литература, 1994.
9. Лукьянов А.Е. Дао “Книги перемен”. – М., 1993.
10. Петухов С.В. Биомеханика, бионика и симметрия. М., Наука, 1981.
11. Петухов С.В. Бипериодическая таблица генетического кода и число протонов. М., 2001.
12. Петухов С.В. Тензорный анализ генетических кодов и геометрическая парадигма биоинформатики. Ежегодник “Дельфис 2005”. М., Дельфис, 2005, с.125-132.
13. Петухов С.В. Геометрические свойства генетического кода и символьная система древнекитайской “Книги перемен”. Геноарт. “MADI. Art periodical” N8, 2006, с. 56.
14. Петухов С.В. Метафизические аспекты матричного анализа генетического кодирования и золотое сечение. – Метафизика (под ред. Ю.С.Владимирова). – Москва, Бином, 2006, с.216-250.
15. Петухов С.В. Матрицы генетического кода и музыка. – Объединенный научный журнал, N13 (173), июнь 2006, с. 46-48.
16. Петухов С.В. Структурные тождества систем генетического кодирования и древнекитайской “Книги Перемен”, – в сб.: Китайская философия и современная наука (под ред. А.Е.Лукьянова). – М., “Луч”, 2006 (в печати).
17. Фейнман Р., Лейтон Р., Сэндс М. Фейнмановские лекции по физике, т.4, М., Мир, 1965.
18. Щуцкий, Ю.К. Китайская классическая “Книга перемен” /Вступительное слово А.И.Кобзева. – М., Восточная литература, 1997.
19. Якимова Н.Н. Смотри в корень. Структурное единство мира. – М., Дельфис, 2005.
20. Bakhtiarov K.I. Logical structure of genetic code. Symmetry: Culture and Science, v. 12, N 3-4, 2001, p.401-405.
21. Cook T.A. The curves of life. – L.: Constable and Co, 1914.
22. Kappraff J., Beyond Measure. Singapore, World Scientific, 2001.
23. Kappraff J., Nexus Network Journal, v.2, N 4, October 2000.
24. Petoukhov S.V. The rules of degeneracy and segregations in genetic codes. The chronocyclic conception and parallels with Mendel’s law’s. – “Advances in Bioinformatics and its Applications” (editors – M.He, G.Narasimhan, S.Petoukhov), Proceedings of the International Conference (Florida, USA, 16-19 December 2004), Series in Mathematical Biology and Medicine, v.8, 2005, pp.512-532, New Jersey-London-Singapore-Beijing, World Scientific.

Данная статья опубликована в ежегоднике “Дельфис”, 2-я часть, 2006 год, с.89-95, материалы Шестой междисциплинарной научной конференции “Этика и наука будущего”.