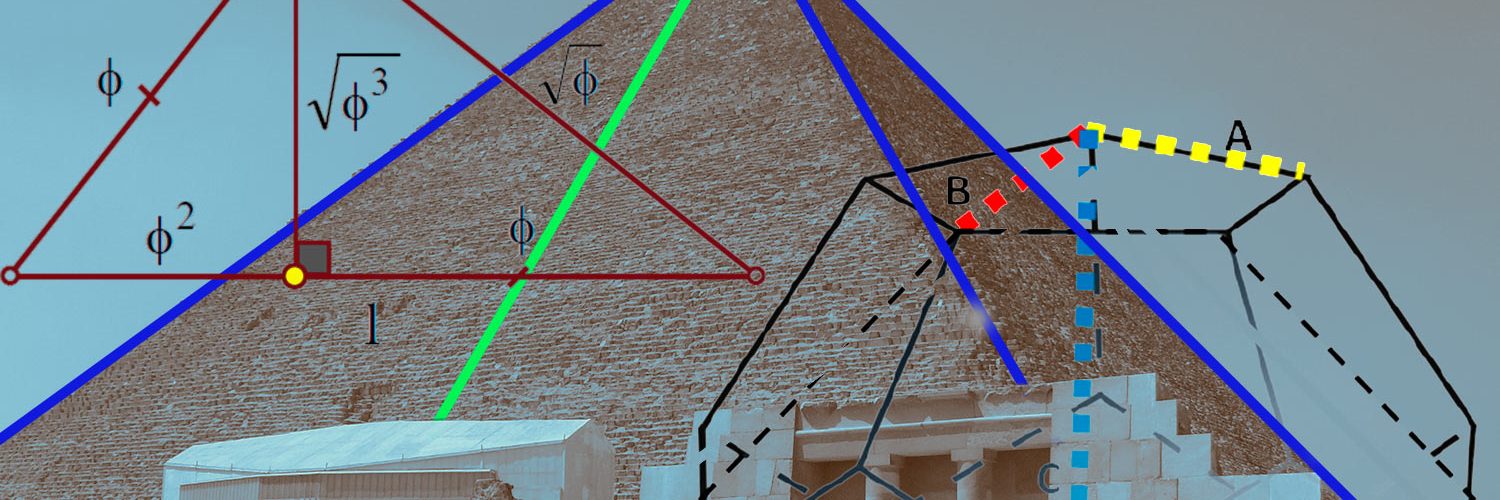
Нами проанализированы существующие данные о размерах боковых поверхностей пирамиды Хуфу и предпринята попытка воспроизвести ее геометрию на основании симметрично расположенных друг на друге трех прямых параллелепипедов с основанием квадрат. Площади квадратов параллелепипедов нами были заданы тремя числами Фибоначчи соотносящиеся больший к среднему, средний к меньшему – как Ф². Больший параллелепипед имеет отношение длины боковой стороны квадрата и его площади к таковой длине и площади среднего квадрата параллелепипеда как Ф²(рисунок 1). Такое же отношение имеет средний по размеру параллелепипед – к меньшему. Длина большего ребра прямоугольника, площадь основания каждого из параллелепипедов соотносится с их меньшей стороной (меньшим ребром прямоугольника боковой поверхности) и его площадью так же – как Ф². Площадь боковой поверхности прямоугольника всех параллелепипедов соотносится к площади вписанного в них квадрата как Ф². Полученная геометрическая композиция их трех параллелепипедов нами спроецирована на двухмерную плоскость поверхности пирамиды Хуфу (см. рисунок 1).

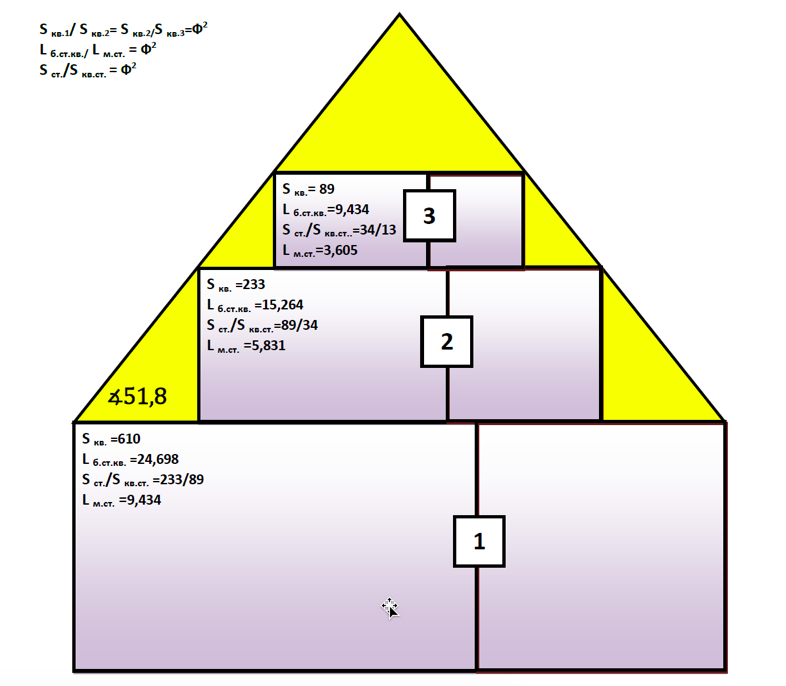
Прямые линии проекции пирамиды Хуфу совпадают с точками ребер (вершинами) трех параллелепипедов расположенных симметрично один над другим, а полученный таким образом угол очень близок к таковому углу, образованным высотой пирамиды Хуфу и половиной ее основания или треугольником Кеплера (≈51,5^○).

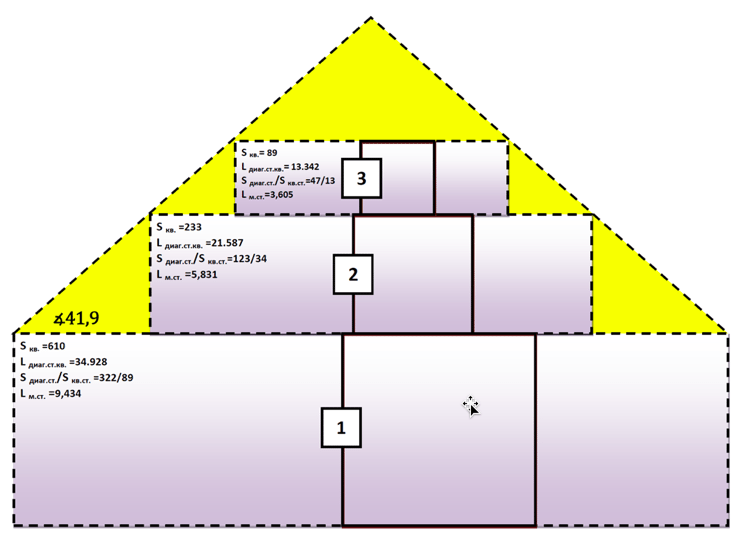
Нами так же построена проекция пирамиды Хуфу на прямые параллелепипеды с основанием квадрат в разрезе по линии диагоналей квадратов (рисунок 2). Таким образом получены линейные размеры поверхностей диагоналей прямых параллелограммов и их площади, которые возросли на значение площади поверхности вписанного в них квадрата и стали равны одному из чисел Люка.Угол, образованный вершинами поверхностей диагоналей построенной нами фигуры и ее основанием, близок к таковому пирамиды Хуфу (≈41,6^○) (см. рисунок 2).

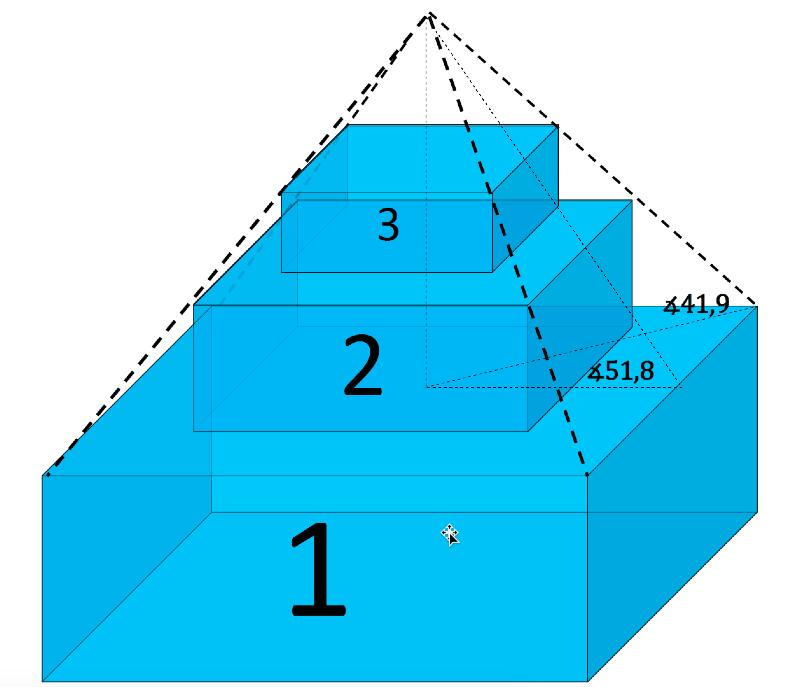
Для наглядного представления предлагаемого способа воспроизведения геометрии пирамиды Хуфу нами нарисована в виде трехмерной модели проекция пирамиды Хуфу на три построенных прямых параллелепипедас основанием квадрат (рисунок 3).

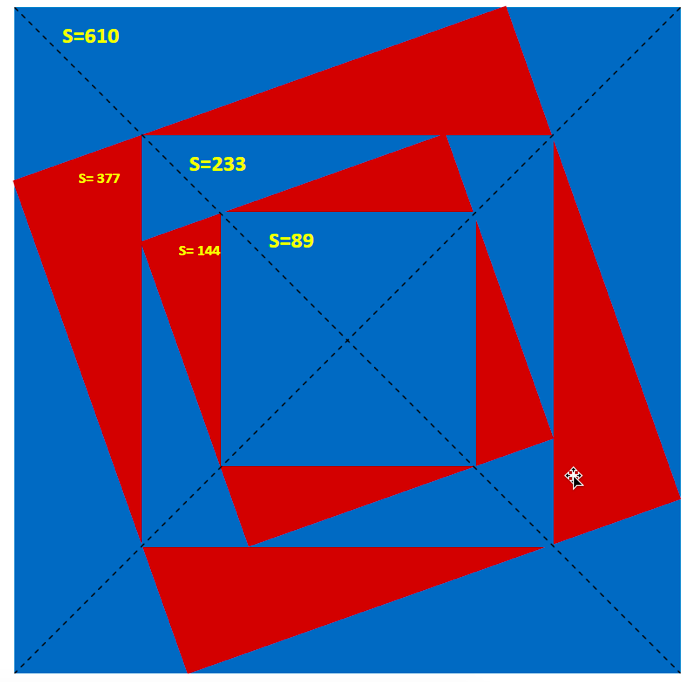
Особенностью предлагаемого нами способа воспроизведения геометрии пирамиды Хуфу является возможность (в качестве универсальной единицы меры) использовать числа Фибоначчи. Например, можно так вписать квадраты оснований предлагаемых нами параллелепипедов, чтобы получить таким образом рекуррентный ряд Фибоначчи из их размеров площадей. Для этого необходимо вписать меньший квадрат с соответствующей площадью размером числа Фибоначчи в больший квадрат вращая при этом их то в одну, то в другую сторону (рисунок 4).

1. Нами проанализированы существующие данные о размерах боковых поверхностей пирамиды Хуфу и воспроизведена ее геометрия на основании симметрично расположенных друг на друге трех прямых параллелепипедов с основанием квадрат.
2. Линии проекции пирамиды Хуфу совпадают с точками ребер (вершинами) трех параллелепипедов расположенных симметрично один над другим, а полученный угол очень близок к таковому углупирамиды Хуфу (≈51,5^○).Угол, образованный вершинами поверхностей диагоналей построенной нами фигуры и ее основанием, близок к таковому пирамиды Хуфу (≈41,6^○).
3. Особенностью предлагаемого нами способа воспроизведения геометрии пирамиды Хуфу является возможность использовать числа Фибоначчи: можно так вписать квадраты оснований предлагаемых нами параллелепипедов, чтобы получить рекуррентный ряд Фибоначчи из их размеров площадей.