«Не следует множить сущее без необходимости». У.Оккам
Известно классическое определение Золотой пропорции как деление отрезка, в котором отношение большей части к меньшей равно отношению всего отрезка – к большей (рисунок 1). Важно отметить в этой связи взаимосвязь трех размерностей. На это же обстоятельство указывает С.А. Алферов, приводит соответствующие уравнения (1) и поясняет [1]: «в последовательности отрезков «a-b-c» средним по длине отрезком является «b». Отсюда понятен смысл одного из старинных определений Золотого сечения, как деления отрезка «на средний и крайний» (а не на два: больший и меньший), то есть – получение взаимосвязи «3-х». На это, без преувеличения, важное уточнение, как нам представляется, сегодня необоснованно мало обращают внимания.
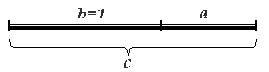
a2 + a – 1 = 0
а1,2 = – 0,5 ± Ц 1,25 (1)
c2 – c – 1 = 0 c1,2 = 0,5 ± Ц 1,25
Это же уравнение, пишет автор [1], возникает при решении следующего прямого треугольника с h=1, условно названного нами в одной из публикаций [5] «треугольник Фибоначчи» (рисунок 2):
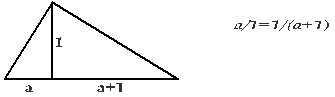
С.А. Алферов формулирует определение Золотого сечения как «соотношение, выраженное двумя числами, дающими «1» в разности и произведении» [1]. Известно отношение в треугольнике Кеплера между гипотенузой и меньшим катетом в виде Золотой пропорции (которые обозначены на рисунке 3 как 1 и ф). К этому следует добавить еще соответствующее отношение меньшего катета ф к меньшему отрезку гипотенузы 1 – ф2. Таким образом мы получаем взаимосвязь трех отрезков в треугольнике Кеплера. Следует отметить, что в треугольнике Кеплера, как и в треугольнике Фибоначчи, возможно выполнить (но не одним и тем же способом) тождество отрезков Золотой пропорции согласно классического определения – а+e≡b (рисунок 3). Следуя изложенной выше логике построения треугольников, мы нарисовали два треугольника: первый – треугольник Кеплера, второй – условно названный нами – «треугольник Фибоначчи» (рисунок 4). Попытки смоделировать иные возможные треугольники, удовлетворяющие определению Золотого сечения как взаимосвязи трех величин отрезков, не принесли положительных результатов.
![Рисунок 3 – Свойства треугольников Кеплера [3] (слева) и Фибоначчи (справа)](https://lah.ru/wp-content/uploads/2018/05/2018-05-06_23-24-05.png)
Треугольник Фибоначчи примечателен еще тем, что позволяет получить определенным образом числа рекуррентного ряда Фибоначчи. Если принять за величину размерности катетов последовательные числа Фибоначчи, то квадрат гипотенузы будет равен соответствующей сумме их квадратов в виде числа Фибоначчи (таблица). Сумма двух последовательных чисел квадратов гипотенузы образуют число рекуррентного ряда Люка. Подобные операции с квадратами катетов треугольника Кеплера (суммирование квадратов с площадью чисел Фибоначчи) выглядят более тривиально.
Таблица – Квадраты чисел рекуррентного ряда Фибоначчи и образуемые определенным суммированием их числа Люка
| Числа ряда Фибоначчи (сумма квадратов) | Числа ряда Люка (сумма) | |
|---|---|---|
| 132+82=233 | ∑ 322 | |
| 82+52=89 | ∑ 123 | |
| 52+32=34 | ∑ 47 | |
| 32+22=13 | ∑ 18 | |
| 22+12=5 | ∑ 7 | |
| 12+12=2 | ||
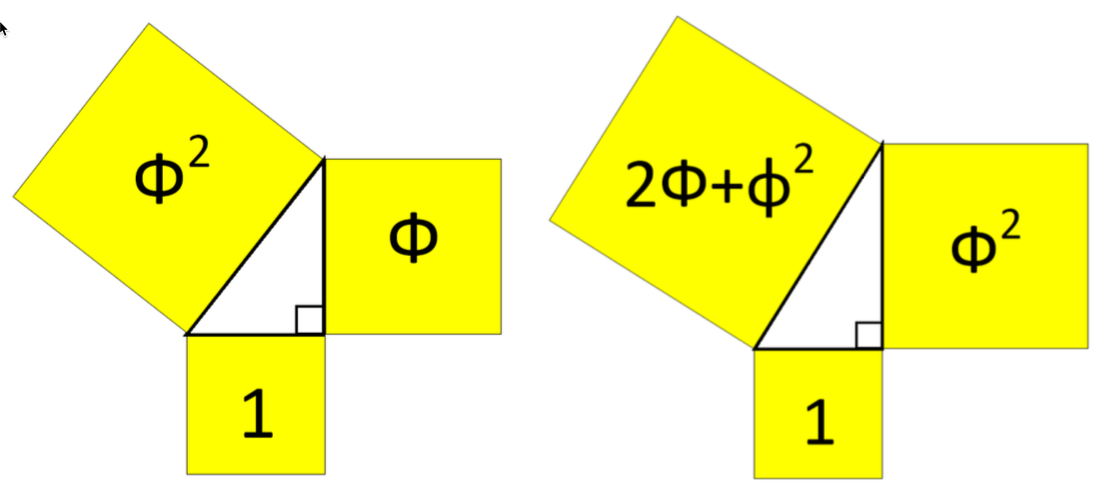
Можно сформулировать две теоремы для рассматриваемых нами треугольников (рисунок 5): для треугольника Кеплера – в прямоугольном треугольнике квадраты катетов площадью 2-х последовательных чисел Фибоначчи, Люка и им подобных рекуррентных рядов образуют квадрат гипотенузы равной площади следующего по порядку числа Фибоначчи, Люка и им и им подобных рекуррентных рядов; для треугольника Фибоначчи – в прямоугольном треугольнике катеты размерностью 2-х последовательных чисел Фибоначчи образуют квадрат гипотенузы равной площади числа Фибоначчи.
Возвращаясь к тематике наших предыдущих публикаций [5, 6, 7] мы задались целью проанализировать связь треугольника Фибоначчи с геометрией пирамиды Хуфу. Первой задачей мы определили проецирование треугольника Фибоначчи на боковую поверхность пирамиды Хуфу с учетом фактического размера гипотенузы треугольника в расчете на единицу измерения «королевский кубит». Исходную величину королевского кубита, как нам представляется, можно принять исходя из двух вариантов, имеющих следующие основания: принять величину, равную 0,524 м, которая кратна размерам помещения пирамиды Хуфу «камера Царя» или – 0,5236067977499784… кратную Ф2. Оба варианта имеют право на существование. Для анализа размеров пирамиды мы выбрали первый вариант на том основании, что величина «королевский кубит» – производная от величины «метр» и в физическом выражении может быть соизмерима с размерами, например, помещения пирамиды «комната Царя». Поэтому получаемая мера кратна длине этого помещения и является рациональным числом. В дальнейшем, при рассмотрении вопросов связанных теорией феномена Золотого сечения мы за искомую величину принимаем второй вариант, который имеет математическое основание – Ф2/5 (2). Полученная мера длины при этом варианте – иррациональное число.
1,6180339887*1,6180339887/5=0,5236067977499784….. (2)
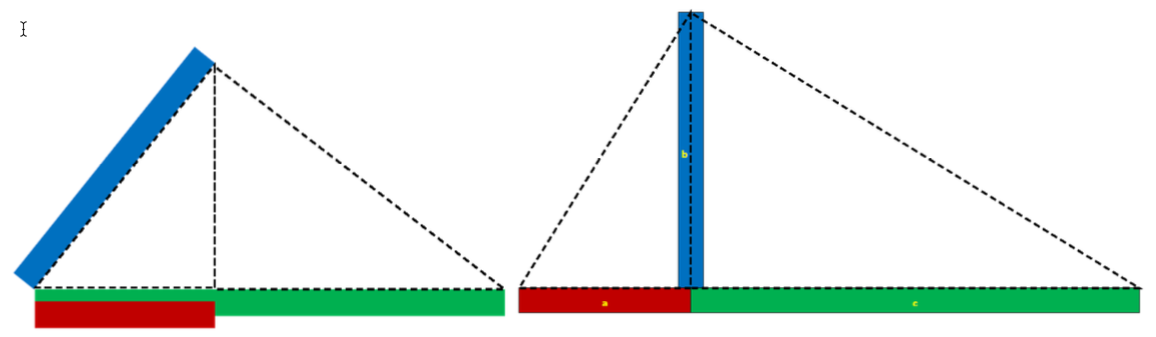
Для расчета фактической длины боковой поверхности основания пирамиды и, следовательно, гипотенузы треугольника Фибоначчи мы построили модель проекции пирамиды Хуфу на первый ряд блоков у ее основания (рисунок 6) с тем расчетом, что: «высота блоков в основании (пирамиды Хеопса – Авт.) составляет 1,41 метра…» [11].
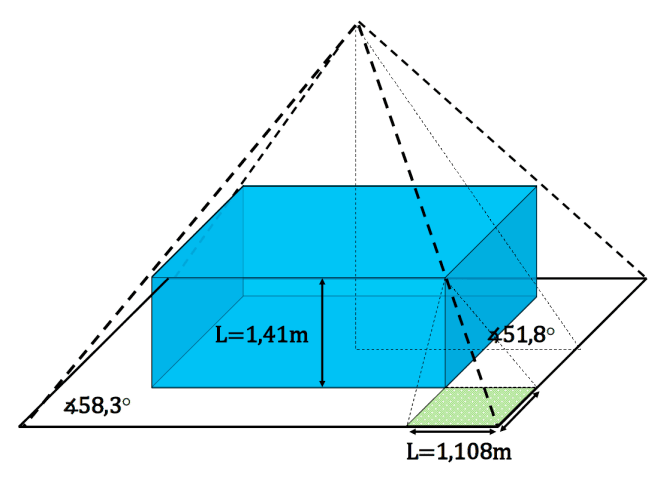
За величину длины боковой стороны первого ряда блоков основания пирамиды мы приняли значение средней арифметической длин всех сторон (3). Полученные посредством проецирования пирамиды Хуфу на первый ряд блоков у ее основания размеры (4) (см. рисунок 6), таким образом, позволяют увеличить длину основания сооружения на 1,10849 м с каждой стороны (5) или на 2,21698 м в целом (6). Итоговая длина основания равна в таком случае 232,5795 м (7) или 443,854 (8) королевских кубита.
230,45+230,25+230,35+230,4=×–230,3625 (3)
1,41/√Ф(1,272018)=1,10849 (4)
1,10849*2=2,21698 (5, 6)
230,3625+2,21698=232,5795 (7)
232,5795/0,524=443,854 (8)
Последующими задачами мы определили: расчет площади основания пирамиды Хуфу в соответствии с полученными размерами основания сооружения при моделировании, проецирование треугольника Фибоначчи на боковую поверхность пирамиды. В этой связи мы провели расчеты:
– возвели в квадрат полученное при моделировании значение длины основания сооружения (9);
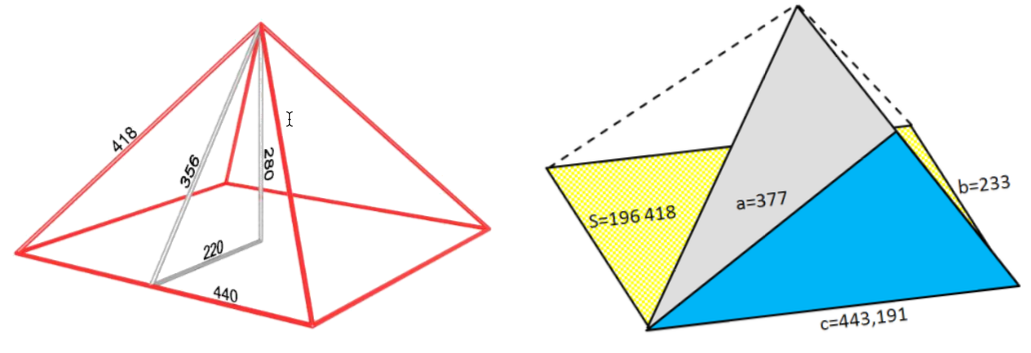
– рассчитали возможный размер гипотенузы треугольника Фибоначчи при соответствующих размерах длин катетов равных последовательным числам Фибоначчи (10) при его проецировании на пирамиду Хуфу (рисунок 7);
– полученную при проецировании длину и квадрат гипотенузы треугольника Фибоначчи (рисунок 7) сопоставили с линейными размерами основания сооружения и его площадью рассчитанными нами при моделировании (см. рисунок 6). Различия между модельными размерами длины и площади основания и расчетными (по треугольнику Фибоначчи) составили: по длине – 0,663 королевского кубита, по площади – 588 квадратных королевских кубита (11). В процентном отношении различия составили менее 0,3% (0,1491948 и 0,298468) от исходной величины.
443,8542=197006 (9) 2332=54289; 3772=142129; ∑(2332+3772)=196418; √196418=443,191 (10)
443,854–443,191=0,663; 197006–196418=588 (11)
В соответствии с существующими данными об отношении площади видимой поверхности пирамиды Хуфу к площади ее основания (=Ф) и исходя из полученных нами данных моделирования проекции пирамиды Хуфу на первый ряд блоков у ее основания (рисунок 6) и сравнения этой модели с проекцией треугольника Фибоначчи (рисунок 7) мы предполагаем, что целочисленное значение площади видимой поверхности пирамиды Хуфу выраженное в единице измерения «квадратный королевский кубит» равно числу Фибоначчи – 317 811 а, площадь всей поверхности пирамиды Хуфу –514229 (12).
196 418*Ф=317 811; 196 418+317 811=514229 (12)
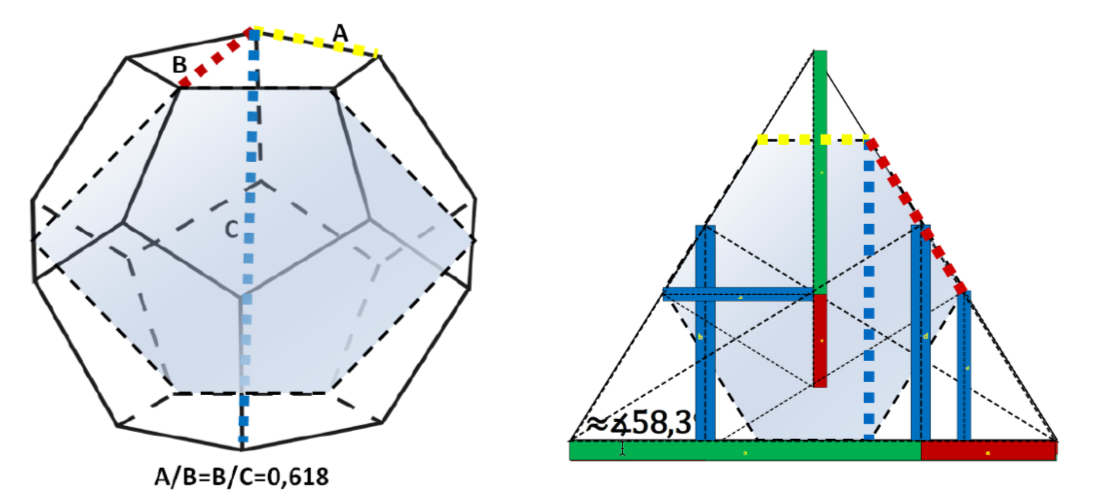
Нами спроецирован так же шестиугольник, полученный при поперечном сечении додекаэдра [2], и выявлено, что угол, образованный основанием и боковой стороной полученного при сечении додекаэдра шестиугольника равен таковому, образованному гранями видимой поверхности пирамиды Хуфу, а длина сторон шестиугольника равна или близка к отношению Золотого сечения (рисунок 8). Выявлено так же, что при наложении треугольника Фибоначчи на смоделированную нами боковую поверхность пирамиды Хуфу существуют совпадения по линиям сторон треугольника с одной стороны, с линиями сторон боковой поверхности пирамиды – с другой (рисунок 8, справа).
Заключительной задачей исследования мы определили нахождение математического основания связи геометрии пирамиды Хуфу и треугольника Кеплера. Считается, что треугольник Кеплера имеет угол в 51,52° при основании и очень близок к таковому в 51,8° пирамиды Хуфу (Хеопса) образованный высотой пирамиды и половиной ее основания. Учитывая данные о существовании вогнутости боковых поверхностей пирамиды Хуфу порядка ≈1 м с каждой стороны (рисунок 9) (условимся – ровно 1 м), можно предположить, что фактические параметры (линейные размеры и величина углов) треугольника образованного половиной длины основания и высотой пирамиды Хуфу равны точно отношению равному √Ф (1,27202..) с учетом рассчитанного нами (посредством проецирования пирамиды Хуфу на первый ряд блоков у ее основания размеры (см. рисунок 6)) увеличения длины основания сооружения на 1,10849 м с каждой стороны. Для этого мы произвели расчеты:
– определили половину длины основания пирамиды исходя из смоделированных нами размеров длины основания в 232,5795 м (13);
– от полученой длины половины основания вычли 1 м длины вогнутости (14);
– определили исходную высоту пирамиды (15) и рассчитали отношение высоты к половине основания (16).
232,5795/2=116,28975 (13)
116,28975-1=115,28975 (14)
280*0,524=146,72 (15)
146,72/115,28975=1,27262 (16)

Любопытное отношение: если рассчитать отношение площади треугольника Кеплера к площади квадрата его основания, то получим – 1,571428571428571 удвоенное значение которого близко к числу π (3,143).
Исходя из полученных нами результатов моделирования и проецирования треугольника Фибоначчи на боковую поверхность пирамиды Хуфу и связи геометрии пирамиды Хуфу и треугольника Кеплера мы выдвигаем гипотезу: при проектировании пирамиды Хуфу архитектор древнего сооружения ориентировался, прежде всего, на геометрию двух треугольников – Кеплера и Фибоначчи; определяющей основой линейных размеров пирамиды Хуфу явились: целочисленные значения катетов треугольника Фибоначчи (выраженных в единице длины «королевский кубит») равных последовательным числам Фибоначчи – 233 и 377, отношение площадей
основания и видимой поверхности сооружения (выраженных в единице площади «квадратный королевский кубит») равных целым числам Фибоначчи (основание – 196418, видимая поверхность – 317811).
Мера «королевский кубит» является, в одно и то же время (!), мерой длины и мерой, кратной отношению квадрата Золотого сечения Ф2 (Ф2/5) или 5*0,5236…= Ф2. Кроме того, эта мера в определенном приближении кратна константе π (π/6). Мера королевского кубита (значение 0,524) кратна длине волны, образуемой частотой Земли в 7,83 Гц (38287/73000≈0,524). Можно констатировать, что посредством меры длины «королевский кубит» – 0,5236… – можно получить безразмерные величины ряда фундаментальных констант, которые представлены иррациональными числами. Например, значения Ф2 (17), π (18), постоянной тонкой структуры (19).
0,5236*5=2,618 (17)
0,5236*6=3,1416 (18)
0,5236*100*2,618=137,07848 (19)
Полученное нами число 137,07848 (19) близко к значению постоянной тонкой структуры (137,036), которая является фундаментальной физической постоянной, характеризующей силу электромагнитного взаимодействия. Постоянная тонкой структуры – безразмерная величина, образованная комбинацией фундаментальных констант. Её численное значение не зависит от выбранной системы единиц. Существует мнение, что постоянная тонкой структуры является классической волновой константой, определяет взаимосвязь корпускулярных свойств электрона с его волновыми свойствами [10].
Следует, в связи со сказанным нами, обратить внимание на единственный рисунок пирамиды Хуфу, который был скрыт над входом в сооружение (рисунок 10). Нами он распознан и интерпретирован как тождество (20). Из данного тождества следует, что величина длины «королевский кубит» – иррациональное число.
5*0,5236≡Ф2 (20)

В связи с вышесказанным важно обратить внимание на определенные логические следствия.
Первое – мера длины «королевский кубит» в численном выражении стала таковой по отношению к мере «метр» и получила значение иррационального числа (Ф2/5) 0,5236…. Следует отметить удобство использования подобного численного иррационального значения меры длины – количество знаков после запятой этого значения меры длины – критерий или требование к точности измерений. В свою очередь, целочисленная мера длины «метр» непосредственно связана своим происхождением с мерой времени – секундой и физической переменной – гравитационным ускорением. Закономерно возникает вопрос: совпадением, случайностью является происхождение меры длины «королевский кубит»? Учитывая высочайший уровень точности пространственной ориентации пирамиды Хуфу по магнитным полюсам Земли, наличие целочисленных значений ее размеров (как мы прояснили в нашей работе) и размеров ее помещений нельзя обоснованно принять в расчет версию о мере длины «локоть» как меры строительства подобного сооружения. Локоть – единица измерения длины, не имеющая определённого значения и примерно соответствующая расстоянию от локтевого сустава до конца вытянутого среднего пальца руки и которую можно произвольно получить без какого-либо инструментария посредством одноименной части тела.
Второе – любая мера, как правило, принимается (отвергая альтернативные меры) в связи с ее удобством использования и получения: меру длины метр можно получить посредством известной конструкции маятника установленного на широте 45 градусов определив его полупериод хода. А вот что касается меры времени – секунды – подобного относительно простого способа сегодня не существует. История происхождения меры времени «секунда» порой противоречива и не определенна. Известно, что жители Древнего Египта делили дневную и ночную половины суток каждую на 12 часов уже, по крайней мере, с 2000 года до н. э. Греческие астрономы периода эллинистической Греции Гиппарх и Птолемей делили день на основе шестидесятеричной системы счисления и также использовали усреднённый час (1⁄24 суток), простые доли часа (1⁄4, 2⁄3 и т. п.) и время- градусы (1⁄360 суток, или 4 современные минуты), но не современные минуты или секунды. Сегодня решено перейти к реализации секунды на основе атомных часов, взяв за основу переход в атомах, слабо подверженных внешнему воздействию – атомах цезия. Существующая мера времени «секунда» (эквивалентна 1/60 минуты, 1/3 600 часа, 1/86 400 суток, 1/31 557 600 юлианского года) обладает, на наш взгляд, важной математической особенностью: знаменатели секунды – большие делители. Например, все делители числа 86400 (1/86 400 суток) – 96 целых чисел (1, 2, 3, 4, 5, 6, 8, 9, 10, 12, 15, 16, 18, 20, 24, 25, 27, 30, 32, 36, 40, 45, 48, 50, 54, 60, 64, 72, 75, 80, 90, 96, 100, 108, 120, 128, 135, 144, 150, 160, 180, 192, 200, 216, 225, 240, 270, 288, 300, 320, 360, 384, 400, 432, 450, 480, 540, 576, 600, 640, 675, 720, 800, 864, 900, 960, 1080, 1152, 1200, 1350, 1440, 1600, 1728, 1800, 1920, 2160, 2400, 2700, 2880, 3200, 3456, 3600, 4320, 4800, 5400, 5760, 7200, 8640, 9600, 10800, 14400, 17280, 21600, 28800, 43200, 86400).
И, наконец, третье – мера длины «королевский кубит» исторически, a priori – величина, предшествующая во времени мере «метр». Доказательством этому утверждению служит сам факт существования пирамиды Хуфу имеющей соответствующие целочисленные значения размеров кратным мере «королевский кубит» и логика получения численного значения иррационального числа этой меры. Безусловно, свое численное выражение в виде иррационального числа мера длины «королевский кубит» получила именно по отношению к мере длины «метр». Как мы говорили ранее, любая мера должна удовлетворять определенным требованиям: связи с фундаментальными физическими константами, простоты получения, распространенности… В этой связи закономерен вопрос: какой из существующих, распространенных физических величин соответствует, связана или будет кратна мера длины «королевский кубит»? Если принять во внимание сформулированную нами гипотезу-предположение о том, что конструкция пирамиды Хуфу представляет определенное техническое устройство связи, назначение которого – передача информации посредством гравитационных волн, то логично в этом случае предположить, что мера длины «королевский кубит» может быть связана с внеземной величиной, например, быть равной
половине длины волны реликтового излучения (и являться кратной, в то же время, размерам пирамиды Хуфу и ее помещений).
Максимум излучения Вселенной зафиксирован при температуре 2,726 К [8]. В соответствии с законом Вина, длина волны фотонов, формирующих эту температуру, равна 1,063 мм (21), что очень близко и кратно длине двух королевских кубитов – 1,048. Кратность длине волны реликтового излучения (неизменного во Вселенной) меры длины «королевский кубит» связывает гипотезу-предположение о предназначении пирамиды Хуфу (как передающего устройства) и происхождения меры длины «королевский кубит» в единое логически связанное непротиворечивое целое.
l2,726 =C’ =2,898×10-3 =1,063мм. T 2,726 (21)
Рассматриваемый нами предмет – феномен Золотого сечения – находится вне рамок существующей научной парадигмы (это обстоятельство следует четко осознавать). В этом заключены определенные трудности формального и реального характера. Формального характера – мы не вправе вести предметное обсуждение по данной тематике на официальных научных мероприятиях и публиковать свои исследования в рецензируемых государственных изданиях. Реального характера – в связи с предыдущим затруднением, вытекает следующее – отсутствие какой-либо поддержки (финансовой, технической) при проведении исследований в этом направлении. Поэтому многие исследователи и проводят технически относительно простые теоретические исследования. Много аналитических материалов по данной тематике и соответственно, за редким исключением (Э.М.Сороко), – мало работ имеющих философский уровень обобщения. В этом смысле нельзя пренебрегать одним из методов познания – дедукции. В этой связи хотелось бы выделить ценные, на наш взгляд, мысли из публикаций С.Л. Василенко и В.Ю. Татур : «Если в глобальном проявлении окружающий мир упорядочен пропорциональными структурами, то велика вероятность, что в его основе лежит именно модель золотого сечения …золотая пропорция выступает в роли структурирующей подосновы»; «…золотая пропорция стала объединяющим началом таких важных характеристик как целое и часть, мера и подобие» [4]; «Космос – целостен. Он состоит из целостных объектов (систем), которые в свою очередь состоят из таких же целостных объектов. Для того чтобы такие объекты не разрушались, их части, тоже целостные объекты, должны сравниваться. Два объекта могут сравниться либо имея третий объект в качестве общей меры, либо имея меру самого себя. Но, чтобы выступать внешней мерой, эта мера самого себя должна иметь общий характер, что может выражаться только в общем законе ее образования для всех сравнивающихся целостных объектов…» [9].
Таким образом, меру Золотой пропорции можно представить как универсальную качественную и количественную характеристику объекта-системы, отражающую его свойства целостности, меру дифференциированности и подобия его частей целому. В этой связи следует подчеркнуть, что мера Золотого сечения – единственная в своем роде и «бывает только одна – первая, она же и последняя». Обобщая сказанное выше, следует отметить, что мы видим в мере Золотого сечения, прежде всего, основополагающее начало, единый принцип порядка (структурирования, формообразования…). Легко поддаться при подобных утверждениях абсолютизации Золотой пропорции. Но, согласитесь, никто и не спорит сегодня, что по своей распространенности в неживой и живой Природе законмерность Золотого сечения по праву конкурирует по всеобщности проявления с законами Диалектики. А по сути, как нам представляется, – является ее единственным выражением. На высоком уровне обобщения сквозь призму Золотого сечения можно «усмотреть» законы «единства и борьбы противоположностей», «отрицания-отрицания», «перехода количественных изменений в качественные». И вопрос о причине и следствии, соподчиненности при рассмотрении пары «диалектические закономерности–закономерность Золотого сечения» открыт, как и открыто еще множество вопросов связанных с материальным носителем меры Золотой пропорции.
Следуя диалектической логике можно представить оба треугольника – Кеплера и Фибоначчи – как пару противоположностей, как бинарные оппозиции… С одной стороны – существуют «единство», а с другой – «противоположность» рассматриваемых нами фигур: единые меры и единство взаимосвязанных отрезков, но различное их расположение; единство их воспроизведения в геометрической фигуре «пирамида Хуфу», но различия в их геометрии…
Если следовать логике высказываний Кеплера и В.Зубова («Архитектурная теория Альберти» (1946)) о Золотом сечении как о чем-то прекрасном, но второстепенном и зависимом, которое без теоремы Пифагора «ничего не стоит» («Золотые отношения» – побочный результат геометрических построений, следствие, а не причина…» [3]), то следует ли из этих высказываний заключение о том, что все объекты-системы, где мы встречаем Золотую пропорцию, имеют в своем основании геометрию Евклида? Не основана ли морфология неживой и живой Природы на «носителях» Золотой пропорции – треугольниках Кеплера и Фибоначчи?
В начале статьи нами не случайно вынесены в эпиграф слова У.Оккама, ставшие сегодня методологическим принципом «Бритва Оккама»: «Не следует множить сущее без необходимости». Именно с этой логикой, как нам представляется, следует подходить к пониманию феномена Золотого сечения. Искренне надеемся, что в нашей работе мы не преумножили сущее.
- Алферов, С. А. Золотая пропорция, треугольник Паскаля и принцип квадр // «Академия Тринитаризма», М., Эл No 77-6567, публ.12706, 13.12.2005
- Алферов, С. А. О взаимосвязях додекаэдра и икосаэдра // «Академия Тринитаризма», М., Эл No 77-6567, публ.14041, 29.11.2006
- Василенко, С.Л. Дуализм «двух сокровищ геометрии»: теоремы Пифагора и золотого сечения // «Академия Тринитаризма», М., Эл No 77-6567, публ.23021, 03.02.2017
- Василенко, С.Л. Дуализм модели золотой пропорции // «Академия Тринитаризма», М., Эл No 77-6567, публ.23987, 23.11.2017
- Ворон, А.В. Геометрический треугольник Фибоначчи и пирамида Хеопса // «Академия Тринитаризма», М., Эл No 77-6567, публ.23546, 13.07.2017
- Ворон, А.В. Культорологический и технологический аспект великой пирамиды // «Академия Тринитаризма», М., Эл No 77-6567, публ.24005, 29.11.2017
- Ворон, А.В. Способ воспроизведения геометрии пирамиды Хуфу на основе использования чисел Фибоначчи // «Академия Тринитаризма», М., Эл No 77-6567, публ.24204, 20.01.2018
- Канарёв Ф.М. Спектр излучения вселенной // http://www.sciteclibrary.ru/texsts/rus/stat/st2950.htm
- Татур, В.Ю. Целое:самоизмерение и самоподобие // «Академия Тринитаризма», М., Эл No 77-6567, публ.22825, 15.12.2016
- Холодов, Л.И., Горячев, И.В. Соображения о физическом смысле постоянной тонкой структуры // «Академия Тринитаризма», М., Эл No 77-6567, публ.21951, 03.04.2016
- Davidovits J., Davidovits F. «The Pyramids. An Enigma Solved». 2-nd revised edition – Институт геополимеризации, Париж, Франция, 2001.
Если вы нашли ошибку, пожалуйста, выделите фрагмент текста и нажмите Ctrl+Enter.














Добавить комментарий