Аннотация

Причиной, побудившей к анализу тождеств ряда двумерных и трехмерных геометрических фигур, стало нахождение уникального, на наш взгляд, геометрического тождества в одной из пирамид комплекса Гизы. Рассматриваются возможные варианты тождеств значений площади и периметра ряда двумерных фигур (квадрата, круга, прямоугольного, равнобедренного и равностороннего треугольников), объема и площади – трехмерных (куба, сферы, тетраэдра, октаэдра, икосаэдра, додекаэдра). Показана уникальность рассматриваемого прямоугольного треугольника с тождественными значениями площади, периметра и квадрата меньшего катета.

Ключевые слова: тождество значений, двумерные фигуры, трехмерные фигуры, параметры геометрических фигур, периметр, объем, площадь.

Введение

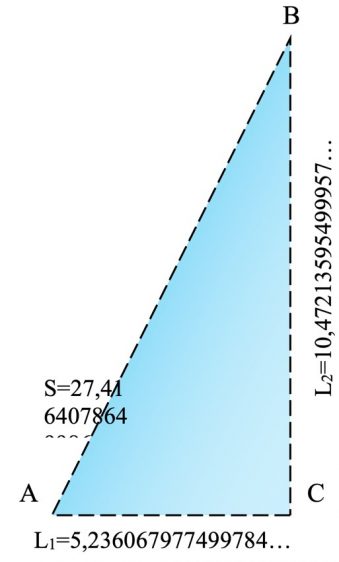
Причиной, побудившей к анализу ряда тождеств двумерных и трехмерных геометрических фигур, стало нахождение уникального, на наш взгляд, геометрического тождества: в одной из пирамид комплекса Гизы – в помещении пирамиды Хуфу «Камера Царя» – по результатам анализа выявлено, что линейные размеры пола помещения вмещают два прямоугольных треугольника со следующими свойствами: значение площади прямоугольного треугольника тождественно значению его периметра (P=27,4164078649986…), а так же – квадрата меньшего катета (27,4164078649986…≡L_м.кат.5,236067977499784…²) [1] (рисунок 1).

Рисунок 1 – Прямоугольный треугольник с тождественными значениями площади, периметра и квадрата меньшего катета: в помещении «Камера Царя» (сверху) и отображенный (снизу)

В этой связи нами сформулированы два вопроса:

– какие существуют тождества площади и периметра у двумерных фигур, объема и площади – у трехмерных?;

– уникально ли тождество площади, периметра и квадрата меньшего катета найденного нами прямоугольного треугольника?

Основная часть

Расчеты параметров ряда двумерных и трехмерных фигур производились преимущественно посредством онлайн калькулятора «Geleot». Расчеты, требующие точности более трех знаков после запятой, производились самостоятельно на основе соответствующих формул, с помощью калькулятора.

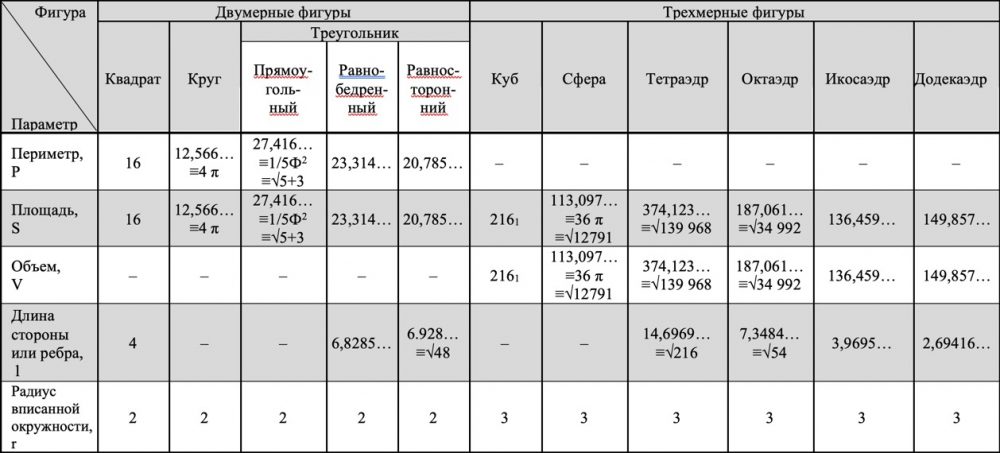
По результатам расчетов выявлены следующие значения тождеств площади и периметра ряда двумерных фигур, объема и площади – трехмерных (таблица):

– квадрата, когда сторона равна 4 (площадь и длина периметра, соответственно, будут тождественны значению 16);

– круга, когда наблюдается тождество площади и длины окружности при значении 12,566… или 4 π (диаметр круга при этом равен значению 4);

– прямоугольного треугольника, когда площадь и длина периметра равна значению 27,416324… или 5,23606…²≡1/5Ф²≡√5+3) – единственный случай, при множестве возможных значений катетов прямоугольного треугольника, когда площадь этой фигуры тождественна (не только периметру) еще и квадрату меньшего из катетов (27,416324… ≡5,23606…²). Подобный случай назван двойным тождеством прямоугольного треугольника;

– равнобедренного треугольника, при значении площади 23,314… (при этом катеты равны 6,8285…);

– равностороннего треугольника, при значении площади 20,785… (при этом длина стороны равна 6.928…≡√48);

– куба, при равенстве объема и площади поверхности куба – 216 (радиус вписанной сферы при этом равен 3, радиус описанной сферы равен √27, диагональ стороны куба – √72, площадь стороны – 36, длина ребер – 72);

– сферы (тождество объема и площади поверхности) равной значению 113,097335526… или 36 π (при этом диаметр сферы равен 6, а ее окружность – 18,85…≡6 π);

– тетраэдра (тождество площади и объема) равной значению 374,123… (при этом длина ребра равна 14,69693845669907…≡√216);

– октаэдра (тождество площади и объема) равной значению 187,061… (при этом длина ребра равна 7,348469228349534…≡√54);

– икосаэдра (тождество площади и объема) равной значению 136,4595… (при этом длина ребра равна 3,9695…);

– додекаэдра (тождество площади и объема) равной значению 149,8578… (при этом длина ребра равна 2,694168…).

В трехмерных фигурах известных как «Платоновы тела» и в фигуре «сфера» радиус вписанной окружности при тождестве площади и объема одинаков (равен 3). В двумерных фигурах квадрат, круг, прямоугольный, равнобедренный и равносторонний треугольник радиус вписанной окружности при тождестве площади и периметра одинаков (равен 2). Обобщением наблюдаемых тождеств является теорема: в правильных двумерных и выпуклых трехмерных геометрических фигурах радиус вписанной окружности (радиус сферы для трехмерных фигур) при тождестве площади и периметра (площади и объема для трехмерных фигур) одинаков (равен 2 для двумерных и 3 для трехмерных).

Таблица – Параметры геометрических фигур, где наблюдается тождество значений площади и периметра для двумерных фигур, объема и площади – для трехмерных.

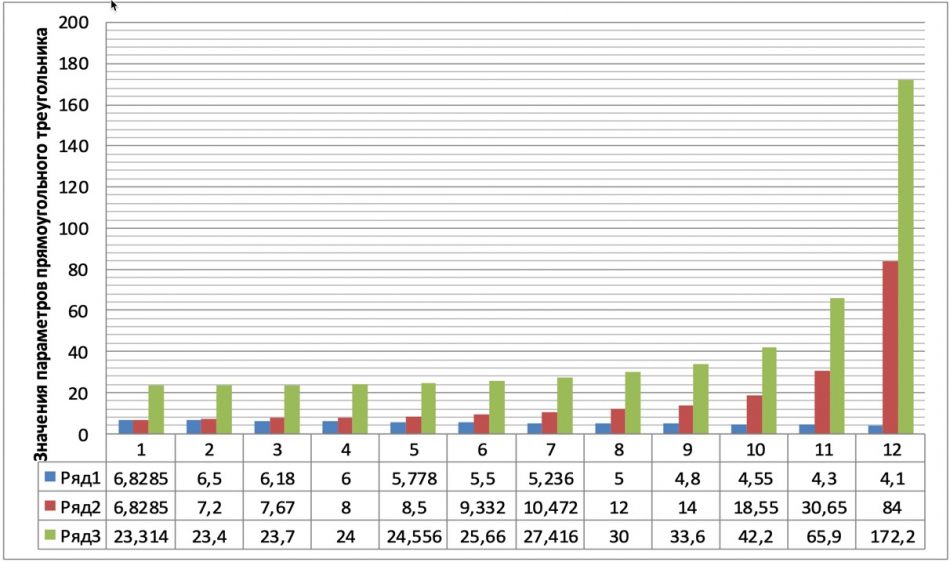
Для разрешения вопроса об уникальности найденного тождества площади и периметра прямоугольного треугольника с катетами равными √5+3 и (√5+3)*2 выявлено 12 различных случаев (среди их множества) тождества площади и периметра прямоугольного треугольника (рисунок 2). Показано, что тождество возникает:

– при нелинейном уменьшении значения меньшего катета (и увеличении другого) с 6,8285… до 4;

– при нелинейном увеличении значения большего катета (и уменьшении другого) с 6,8285… до ∞;

– при нелинейном увеличении значения площади со значения 23,314… (равнобедренный треугольник с катетами 6,8285…) до ∞.

Таким образом, по результатам расчетов и анализа, уникальность рассматриваемого нами прямоугольного треугольника с тождественными значениями площади, периметра и квадрата меньшего катета подтверждается фактом единственного представления его со свойствами двойного подобия среди прямоугольных треугольников с тождественными значениями площади и периметра.

Рисунок 2 – Диаграмма значений катетов и площади прямоугольных треугольников, где тождественны значения периметра и площади фигуры: ряд 1 – меньший катет; ряд 2 – больший катет, ряд 3 – площадь фигуры

Заключение

1. Рассмотрены возможные варианты тождеств значений площади и периметра ряда двумерных фигур (квадрата, круга, прямоугольного, равнобедренного и равностороннего треугольников), объема и площади – трехмерных (куба, сферы, тетраэдра, октаэдра, икосаэдра, додекаэдра).
2. В трехмерных фигурах известных как «Платоновы тела» и в фигуре «сфера» радиус вписанной окружности при тождестве площади и объема одинаков (равен 3). В двумерных фигурах квадрат, круг, прямоугольный, равнобедренный и равносторонний треугольник радиус вписанной окружности при тождестве площади и периметра одинаков (равен 2).
3. Показана уникальность рассматриваемого нами прямоугольного треугольника с тождественными значениями площади, периметра и квадрата меньшего катета. Подобный случай определен как «двойное тождество прямоугольного треугольника».

Список литературы

1. Ворон, А.В. Мера длины «Королевский кубит» и позиционная система счисления с иррациональным основанием // «Академия Тринитаризма», М., Эл № 77-6567, публ.25842, 01.11.2019