Введение

На основе теоретического анализа квадратов Кхаджурахо, Дюрера и подобных им квадратов 4×4 выявлены особенности их «структуры»: инвариантами строения пандиагональных квадратов 4×4 являются пары чисел равные в сумме одному из двух чисел Фибоначчи – 13 или 21.

Магический квадрат – квадратная таблица n×n, заполненная n²различными числами таким образом, что сумма чисел в каждой строке, каждом столбце и на обеих диагоналях одинакова. Самый ранний уникальный магический квадрат 4×4 обнаружен в надписи XI века в индийском городе Кхаджурахо. Квадрат 4×4, изображённый на гравюре Альбрехта Дюрера «Меланхолия», считается самым ранним в европейском искусстве (1514г.). Сумма чисел квадрата Дюрера на любой горизонтали, вертикали и диагонали равна 34. Эта сумма также встречается во всех угловых квадратах 2×2, в центральном квадрате, в квадрате из угловых клеток, в квадратах, построенных «ходом коня» (2+12+15+5 и 3+8+14+9), в вершинах прямоугольников, параллельных диагоналям (2+8+15+9 и 3+12+14+5), в прямоугольниках, образованных парами средних клеток на противоположных сторонах (3+2+15+14 и 5+8+9+12). Большинство дополнительных симметрий связано с тем, что сумма любых двух центрально симметрично расположенных чисел равна 17.

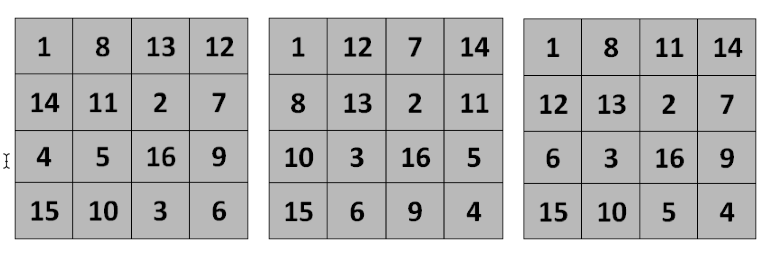
Существует 48 пандиагональных квадратов 4×4 с точностью до поворотов и отражений. Если принять во внимание ещё и симметрию относительно торических параллельных переносов, то остаётся только 3 существенно различных квадрата (рисунок 2).

Основная часть

Мною проанализирована «структура» пандиагональных квадратов 4×4 и выявлены инвариантные части их строения (рисунок 3). Инвариантами строения пандиагональных квадратов 4×4 являются пары чисел равные в сумме одному из двух чисел Фибоначчи – 13 или 21. Различные варианты симметричного комбинирования этих числовых пар образуют множество пандиагональных квадратов 4×4.

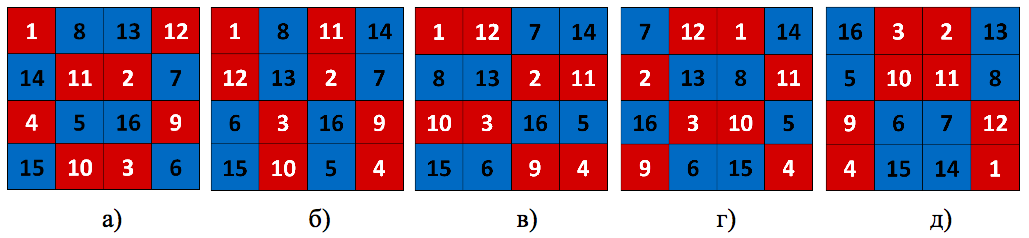
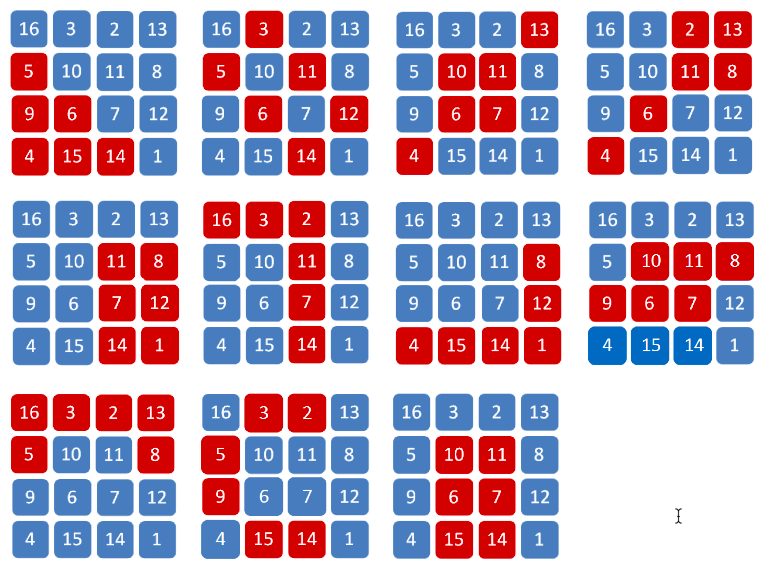
Квадрат Дюрера (и ему подобные пандиагональные квадраты 4×4) обладают симметрией золотой пропорции. Например, на рисунке 4 показано красными и синими квадратами варианты симметрий, при которых среднее арифметическое значение от суммы красных составляющих квадратов в возможных позициях (4 или 2, при вращении в разные стороны) равно 51. Таким образом, сумма всех чисел квадрата – 136, из которых 85 – синие, 51 – красные. 136/85=1,6; 85/51=1,667.

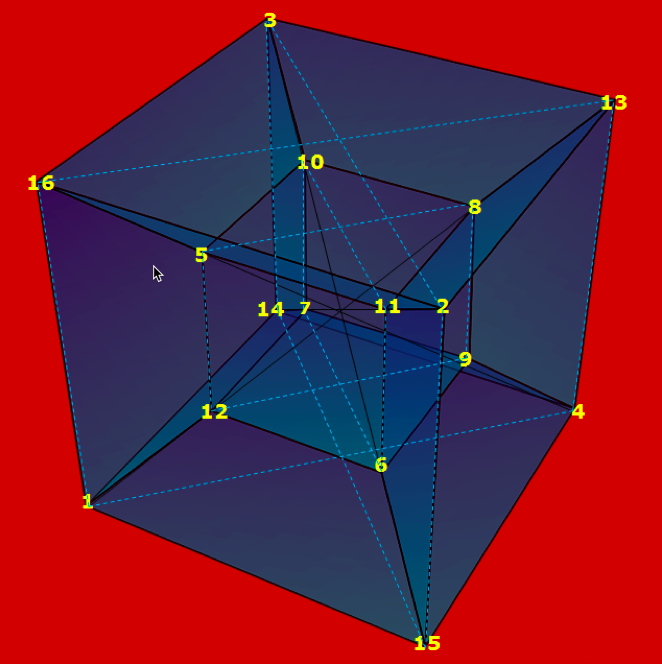
На основе квадрата Дюрера нами построена геометрическая фигура «куб в кубе», обладающая свойствами симметрии пандиагональных квадратов 4×4 (рисунок 5). Подобное «преобразование» стало возможным при расположении вертикальных столбцов чисел квадрата Дюрера под определенным углом, образуя, таким образом, куб в кубе. При этом свойствами «золотой симметрии» обладают все числа диагоналей куба (два числа образуют в одном случае – в сумме число 13, в другом – 21), а все плоскости, имеющие 4 угла (числа) как внутреннего, так и внешнего квадратов построенной фигуры образуют в сумме число Фибоначчи – 34.

Заключение

1. На основе теоретического анализа пандиагональных квадратов 4×4 показаны их особенности «структуры»: инвариантами строения пандиагональных квадратов 4×4 являются пары чисел равные в сумме одному из двух чисел Фибоначчи – 13 или 21.
2. Выявлено, что любой вариант множества шести цифр квадрата Дюрера и ему подобных пандиагональных квадратов 4×4, образующих непрерывную симметричную конфигурацию, равен в сумме целому числу – 51.
3. Построена геометрическая фигура «куб в кубе», обладающая свойствами «золотой симметрии» пандиагональных квадратов 4×4. Свойствами «золотой симметрии» обладают все числа диагоналей куба (два числа образуют в одном случае – в сумме число 13, в другом – 21), а все плоскости, имеющие 4 угла (числа) как внутреннего, так и внешнего квадратов геометрической фигуры образуют в сумме число Фибоначчи – 34.