Цивилизация Древнего Египта периода фараонов строилась на руинах гораздо более древней очень высокоразвитой цивилизации, уровень которой превосходил даже наше современное общество
А.Ю. Скляров
Аннотация
Рассматривается версия о предназначении комплекса пирамид Гизы как своеобразного земного «Вояджера» представителей развитой цивилизации, который спроектирован и построен специально для передачи сведений будущим поколениям и одновременно является передающим устройством связи. На основании предположения были поставлены вопросы: каким образом может быть сформулировано «послание» и каким способом это послание может быть «прочитано»? Мы предположили, что «послание» может быть сформулировано и «прочитано» нами в виде универсального «языка» формальной логики, геометрии и математики. Выявлено, что значения системы мер в Древнем Египте кратны по отношению к мере «Локоть царский» (=0,5235 м), а мера длины используемая при строительстве пирамиды Хуфу – иррациональное число 0,523606… . В связи с предположением о «послании» мы подвергли анализу геометрические размеры помещения пирамиды Хуфу «Камера Царя». Важным результатом анализа стало выявление тождества в виде равенства значений площади треугольника (образованного шириной и длиной помещения пирамиды «камера Царя» и выраженное в единице длины «Метр») и периметра этого же треугольника в тех же единицах длины. Сформулирована гипотеза о владении строителями пирамид двумя мерами длины «Королевский кубит», «Метр» и существовании некого технического средства с системой счисления с иррациональным основанием. Показано, что современные системы счисления имеют существенный недостаток в виде нулевой избыточности кода в отличие от систем счисления с иррациональным основанием. На основании Фибоначчиевой системы счисления и меры «Королевский кубит» нами разработана система счисления с основанием в виде иррационального числа 0,523606… и показана ее оптимальность для операций счисления в одноименных единицах меры длины.
Ключевые слова: мера длины, Королевский кубит, царский локоть, система счисления, иррациональное основание, золотое сечение, цивилизация, Камера Царя, пирамида Хуфу.
Введение
Возвращаясь к более ранним публикациям, мы уже высказывали теоретически обоснованные предположения о том, что проект «комплекс пирамид Гизы» – это своеобразный «Вояджер» представителей развитой цивилизации, который спроектирован и построен специально для передачи сведений будущим поколениям или цивилизации [2]. Кроме того, было математически доказана связь геометрии пирамиды Хуфу и чисел Фибоначчи: основание и видимая поверхность сооружения равна 27 и 28 числу рекуррентного ряда Фибоначчи, а геометрию пирамиды Хуфу можно воспроизвести на основе использования чисел Фибоначчи [3, 4]. В одной из публикаций [1] нами на основании анализа линейных значений расстояний между геометрическими центрами помещений (их взаимного расположения) Красной пирамиды, помещений комплекса пирамид Гизы сделано теоретическое предположение о назначении комплекса пирамид как единого устройства связи (так как подобное взаимное расположение помещений может быть обусловлено положительным эффектом фазированной антенны). Таким образом нами получены предпосылки и логические основания для формулирования рабочей гипотезы о предназначении комплекса пирамид Гизы как своеобразного земного «Вояджера» содержащего непосредственно «послание» и средство связи – некоторое техническое сооружение-устройство.
Следуя предположению А.Ю. Склярова о существовании до цивилизации человечества более развитой цивилизации и в рамках версии о предназначении комплекса пирамид Гизы как своеобразного земного «Вояджера» мы сформулировали ряд вопросов:
– каким образом может быть сформулировано «послание»?;
– каким способом послание может быть «прочитано»?
Основная часть
1. Мера длины «Королевский кубит»
Пытаясь найти ответ на поставленные вопросы, мы предположили, что послание может быть сформулировано и «прочитано» нами в виде универсального «языка» формальной логики, геометрии и математики. В этой связи мы подвергли анализу геометрические размеры, параметры помещения пирамиды Хуфу «Камера Царя». И, прежде всего, мы желали выяснить – на основании какой единицы меры длины было спроектировано (в частности) помещение пирамиды «Камера Царя».
Известно, что «кубит» (царский локоть) – мера длины древних египтян, широко применявшаяся в строительстве. Во времена правления фараона Хуфу (Хеопса) при постройке пирамиды применялся так называемый «королевский кубит» или «локоть царский». 1 «кубит» был равен приблизительно 52,4 сантиметров (интервал от 0,5235 до 0,524 м). Достоверно известно так же, что размеры помещений пирамиды Хуфу (как и помещения множества других пирамид) имели целочисленные значения, выраженные в единицах длины «локоть царский» (далее по тексту – «Королевский кубит»).
В одной из публикаций [3] нами предлагается расчет точного значения меры «Королевский кубит», которое можно вычислить исходя двух способов: из √5+3/10 и из значения квадрата золотого сечения «Ф2» деленного на 5 (1). Согласно нашему предположению суть второй математической операции отображена на единственном рисунке пирамиды Хуфу, расположенном над входом в сооружение, который был до недавнего времени скрыт (рисунок 1). Нами он распознан и интерпретирован как тождество (2) [3]. Из данного тождества следует, что величина длины «Королевский кубит» – иррациональное число.
Рисунок 1 – Надпись над входом в пирамиду Хуфу (фотоснимок)
2,618033988749892… /5=0,5236067977499784… (1)
5*0,523606…≡Ф2. (2)
Известно, что в древнем Египте единица длины «Королевский кубит» делилась на 7 ладоней (74,8 мм) или 28 пальцев (18,7 мм). В этой связи мы подвергли делению полученное значение меры «Королевский кубит» на, соответственно, значения 7 (3) и кратное ему 28 (4).
0,5236067977499784…/7=0,0748009711071398… (3)
0,5236067977499784…/28=0,0187002427767849… (4)
По нашему мнению, подобное деление (3) (4) меры «Королевский кубит» имеет рациональное основание – делимые части кратны числу 0,0187 практически без остатка (по 1/7=0,0748002… и 1/28=0,0187009..).
В связи с исследованием меры длины «Королевский кубит» нами проанализированы значения системы мер длины в Древнем Египте (с V по I век до нашей эры) (таблица 1).
Таблица 1 – Система мер длины в Древнем Египте (с V по I век до нашей эры)
| Мера длины | Единица длины, м | Значение дроби меры «Локоть царский»=0,5235 м |
| Атур обычный | 5235 | 1/10000 |
| Атур царский | 10470 | 1/20000 |
| Парасанг | 6980 | 1/13333,3333… |
| Шем | 6282 | 1/12000 |
| Миля | 1745 | 1/3333,3333… |
| Стадий* | 174,5 | 1/333,3333… |
| Стадий | 209,4 | 1/400 |
| Хет (сенус) | 52,35 | 1/100 |
| Оргия | 2,09 | 1/4 |
| Ксилон | 1,57 | 1/3 |
| Дихас | 0,1745 | 1/0,3333… |
| Шесп | 0,08725 | 1/0,1666… |
Выявлено, что значения системы мер кратны или имеют соответствующее значение дроби по отношению к мере «Локоть царский» (=0,5235 м). Таким образом, можно предположить, что основой системы мер длины в Древнем Египте (с V по I век до нашей эры) являлся «Локоть царский». Эта мера по численному выражению достоверно не отличается от значения иррационального числа полученного при делении значения квадрата золотой пропорции на 5 (1).
Для подтверждения предположения о повсеместном использовании в строительстве в Древнем Египте меры длины «Королевский кубит» нами проанализированы линейные размеры объектов план-схемы Саккарского Серапеума (рисунок 2). Не известно, насколько точным является этот план (единственно доступный из источников план), но мы посчитали необходимым его использование. На основании существующего размера масштаба, мы посредством компьютерного программного обеспечения, пересчитали указанные в единицах длины «Метр» на единицы длины «Королевский кубит» (0,523606… м). В результате, нами получен ряд целочисленных значений расстояний между объектами Саккарского Серапеума (центрами саркофагов и расстояний между ними), а так же – расстояний между помещениями. Все расстояния оказались выражены в целочисленных значениях меры длины «Королевский кубит» (0,523606… м).
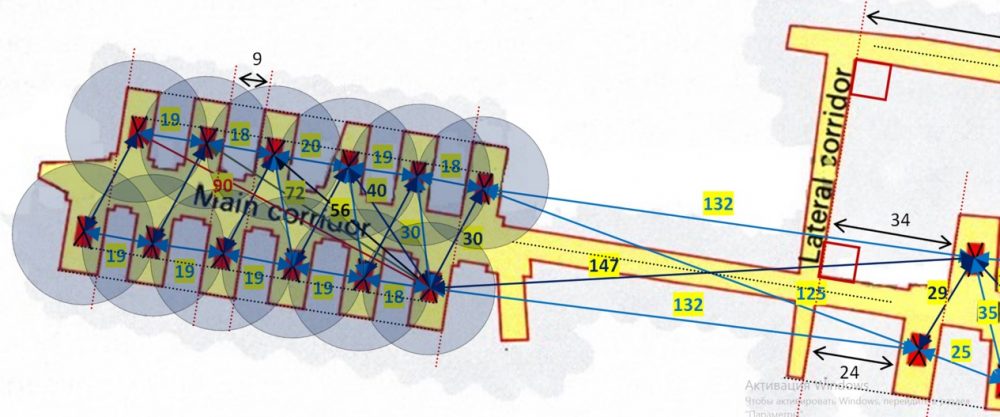
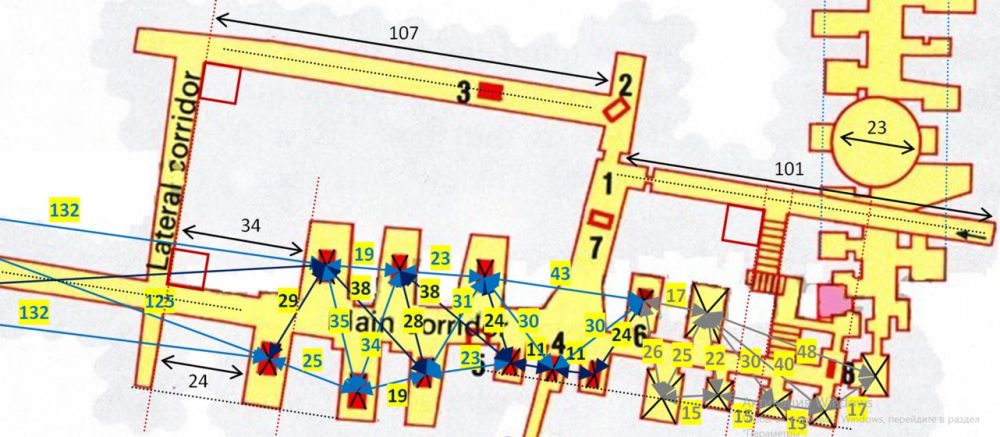
Рисунок 2 – План-схема Саккарского Серапеума:
А) – вид левой стороны; Б) – вид правой стороны.
Размеры указаны в единице длины «Королевский кубит» (0,523606… м)
В связи с проводимым исследованием следует отметить, что иррациональное значение меры «Королевский кубит» (1) еще и кратно значениям (или достоверно близко к ним) двух фундаментальных констант – значению «π» (3,1415926535…) (5) и значению постоянной тонкой структуры (137,036…) (6).
0,5236…*6=3,1416… (5)
0,5236…*100*2,61803…=137,07848… (6)
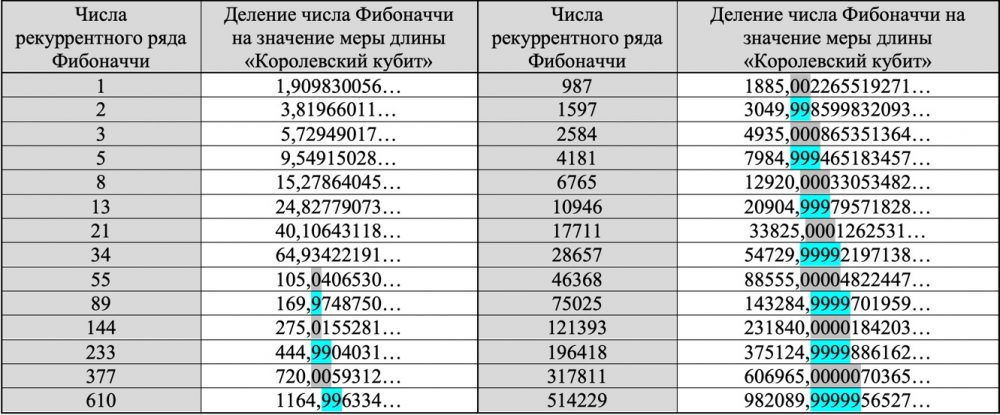
Значение числа меры «Королевский кубит» (0,523606…≡1/5 Ф2) через константу золотого сечения (Ф) непосредственно связано с числами рекуррентного ряда Фибоначчи (таблица 2). Известно, что рядом расположенные числа ряда Фибоначчи имеют отношение близкое к константе золотой пропорции, а через одно число – квадрату золотой пропорции. Исходя из тождества – 0,523606…≡1/5 Ф2 – с увеличением значения числа Фибоначчи (а отношение соседних чисел при этом приближается к константе золотой пропорции) можно получить при делении числа Фибоначчи на значение меры длины «Королевский кубит» рекуррентный ряд с целочисленными значениями 720, 1165, 1885 и так далее. 1/5 от значения каждой цифры этого рекуррентного ряда – число Фибоначчи.
Таблица 2 – Взаимосвязь чисел Фибоначчи и меры длины «Королевский кубит»
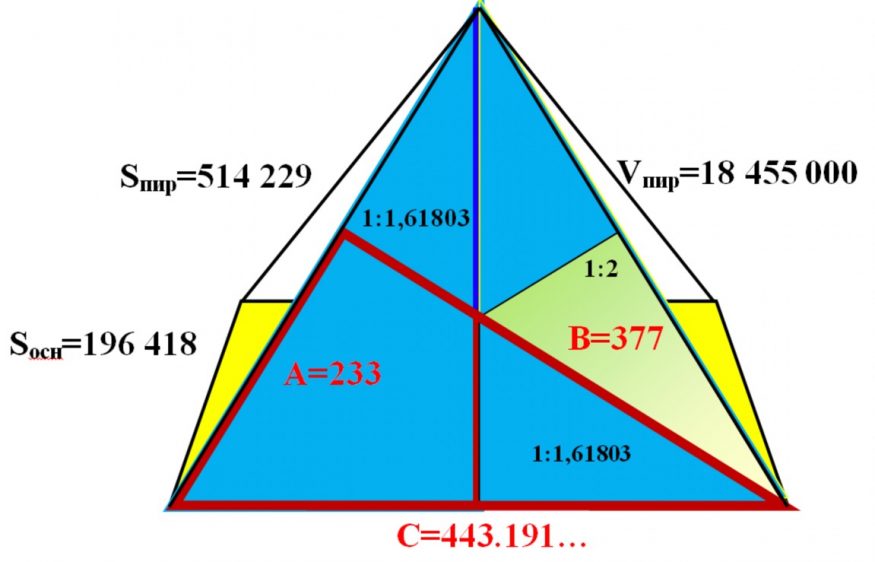
Геометрию пирамиды Хуфу можно воспроизвести посредством использования чисел Фибоначчи: основание и видимая поверхность сооружения равна 27 и 28 числу рекуррентного ряда Фибоначчи, которые выражены в единицах измерения меры площади – квадратах «Королевского кубита» (далее – К.к.2) (Рисунок 3). Таким образом, основание пирамиды Хуфу, согласно расчетам [3], составляет 196418 К.к.2, видимая поверхность – 317811 К.к.2, вся поверхность – 514229 К.к.2. Объем пирамиды Хуфу равен 18455000 К.к.3.
Рисунок 3 – Особенности геометрии пирамиды Хуфу и размеры сооружения, выраженные в единице длины «Королевский кубит» (0,523606…м)
На основании приведенных выше примеров нахождения мер длины кратных мере «Королевский кубит», мы показали, что с высокой степенью вероятности использовалась при проектировании помещения пирамиды Хуфу «Камера Царя» единица меры длины «Королевский кубит».
Для анализа линейных размеров помещения, в дальнейшем, в рамках версии о возможных альтернативных мерах длины при строительстве, мы использовали три меры длины: «Королевский кубит» (0,5236…м); производную от меры «кубит» – меру, кратную 5 мерам «кубит» – Ф2 (2,61803…м); «Метр» (1 м). Выбор трех мер длины для исследования – «Королевский кубит», «Ф2» (2,61803…м) и «Метр» (1 м) – обусловлен их непосредственной связью с константой золотого сечения (1,61803…): первое значение меры длины – это значение пятой части квадрата золотой пропорции, второе – квадрат золотой пропорции, а третье – исходная единица, по отношению к которой две первые меры получили свои «золотоносные» значения.
Анализу подлежали линейные размеры помещения пирамиды Хуфу «Камера Царя». В частности, нами проанализированы (образованные линейными размерами помещения «Камера Царя») геометрические параметры прямоугольных треугольников, которые выражены в трех единицах длины: «Ф2», «Метр» и «Королевский кубит». На рисунке 4 представлены искомые значения прямоугольных треугольников.
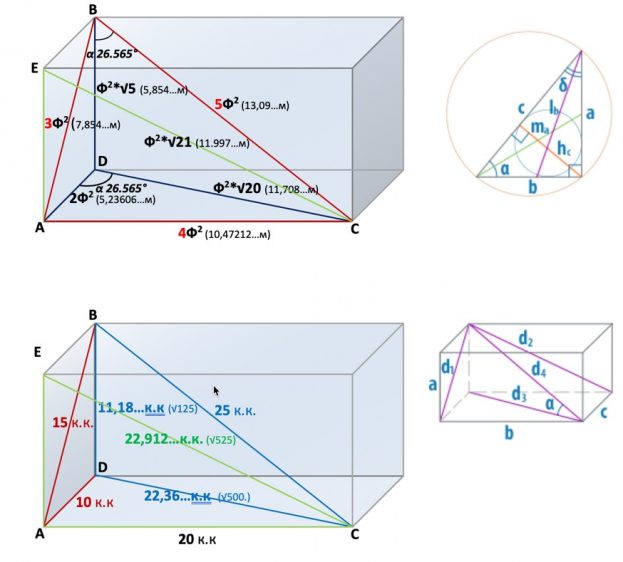 Рисунок 4 – Параметры прямоугольных треугольников Камеры Царя, выраженные в единицах длины: «Ф2» и «Метр» (сверху); «Королевский кубит» [11] (снизу)
Рисунок 4 – Параметры прямоугольных треугольников Камеры Царя, выраженные в единицах длины: «Ф2» и «Метр» (сверху); «Королевский кубит» [11] (снизу)
Расчеты параметров прямоугольных треугольников (параллелепипеда помещения «Камеры Царя») производились преимущественно посредством онлайн калькулятора Geleot. Расчеты, требующие точности более трех знаков после запятой, производились самостоятельно на основе геометрических формул, с помощью калькулятора. Расчету, на основе трех мер длины, подлежали параметры параллелепипеда помещения «Камера Царя» и треугольников, образованных геометрией этого помещения (гипотенуза, площадь, периметр, угол α, угол β, высота, медиана, биссектриса, радиус вписанной и описанной окружности). Результаты расчетов представлены в четырех таблицах (таблицы 3, 4, 5, 6).
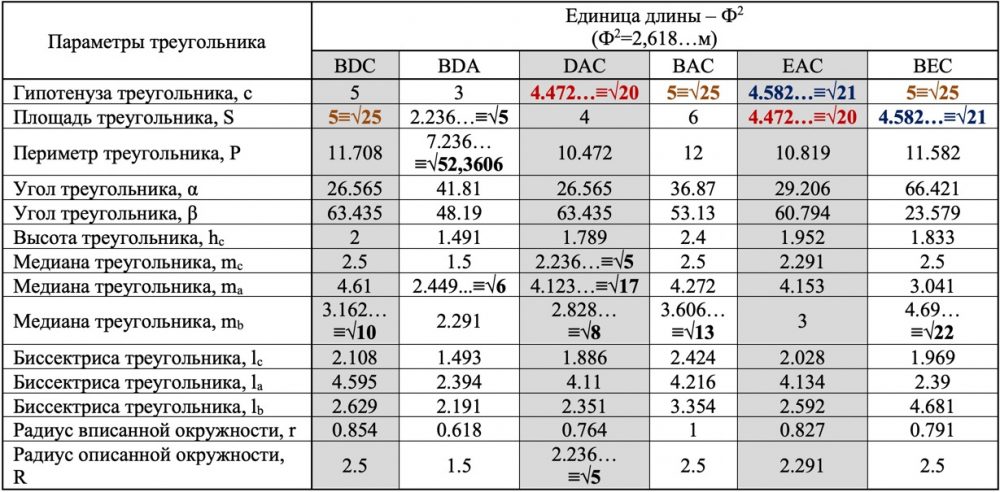
Таблица 3 – Параметры прямоугольных треугольников Камеры Царя, выраженные в единицах длины «Ф2»
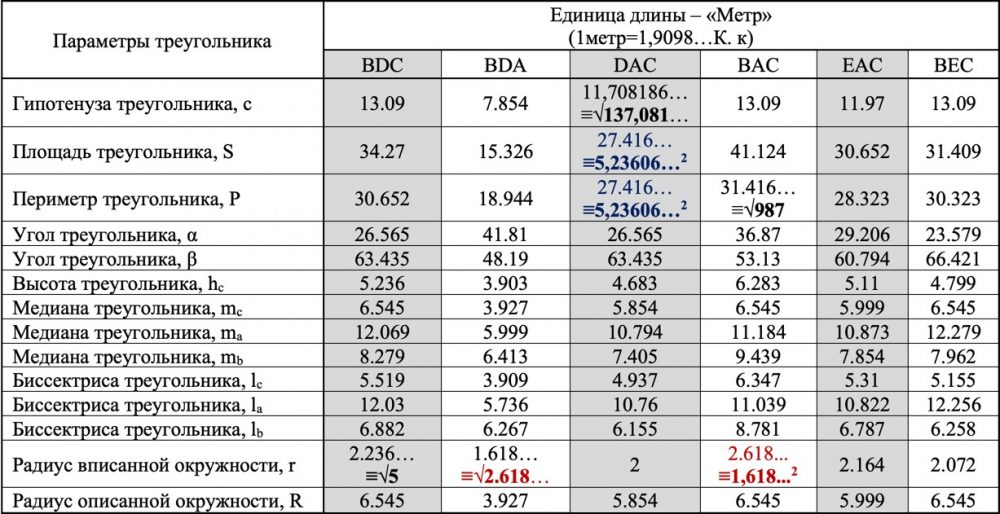
Таблица 4 – Параметры прямоугольных треугольников Камеры Царя, выраженные в единицах длины «Метр»
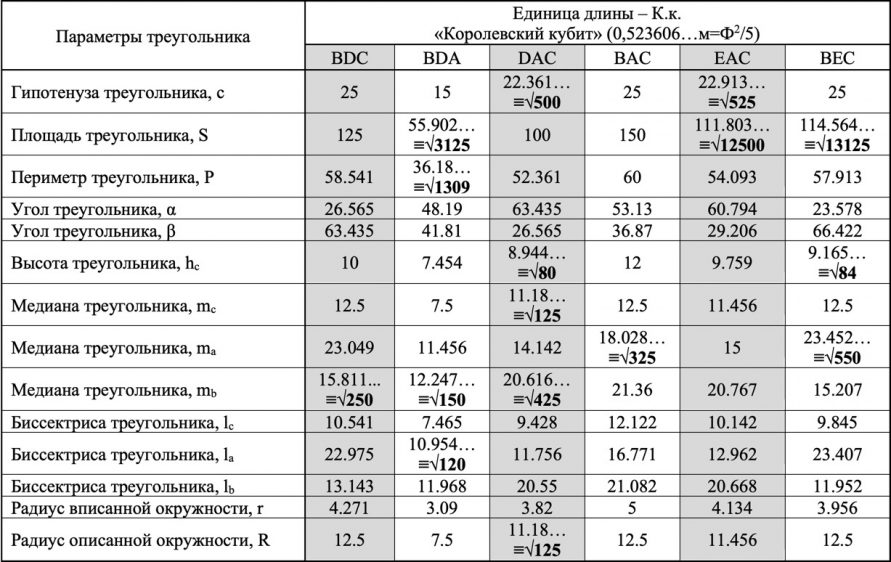
Таблица 5 – Параметры прямоугольных треугольников Камеры Царя, выраженные в единицах длины «Королевский кубит»
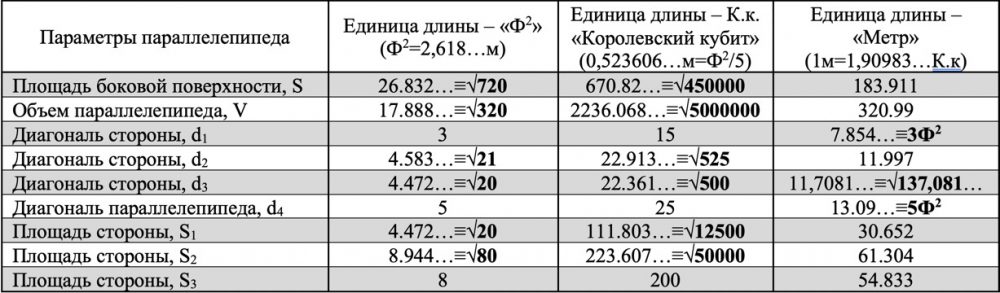
Таблица 6 – Параметры параллелепипеда Камеры Царя, выраженные в единицах длины «Ф2», «Королевский кубит», «Метр»
Анализ полученных данных расчета параметров параллелепипеда (таблицы 3, 4, 5, 6) помещения «Камера Царя» и треугольников, образованных геометрией этого помещения (рисунок 4) выявил:
- Медиана (ma) треугольника «ВDА» = медиане (mс) треугольника «ЕАС» (рисунок 4; таблицы 3, 4, 5);
- Высота треугольника «ВDС» (hc 5,236…) = длине ребра, а ребра «АD» – = удвоенному значению ребра «АС» (рисунок 4; таблицы 3, 4, 5);
- Ребро «BD»/диагональ «DC» = ребро «DА»/ребро «АС» (рисунок 4; таблицы 3, 4, 5);
- Угол треугольников (α) «ВDС» и «DAC» = tg 0,5 (рисунок 4; таблицы 3, 4, 5);
- Гипотенуза треугольника «DAC» = 11,70818609426755… м ≡√137,081621618… (рисунок 4; таблица 4). Получаемое значение от произведения значения одного Королевского кубита на число 100 и затем – на значение Ф2 (0,5236067977499784…*100*2,61803…) (4) равно иррациональному значению 137,081621618… и тождественно длине гипотенузы треугольника «DAC» (таблица 4). Полученное значение близко к значению безразмерной величины – постоянной тонкой структуры (фундаментальной физической постоянной, характеризующей силу электромагнитного взаимодействия = 137,036…).
- Значение площади треугольника «DAC», выраженное в единице длины «Метр», в точности равно периметру этого же треугольника (27,4164078649986…) и тождественно квадрату числа меры длины «Королевский кубит» умноженное на 10 (27,4164078649986…≡5,236067977499784…2) (рисунок 4; таблица 4).
- Периметр треугольника «ВАC» равен значению корня квадратного из 16-го числа Фибоначчи (P=31.416…≡√987) (рисунок 4; таблица 4).
- Два прямоугольных треугольника «ВDА» и «ВАC» параллелепипеда помещения «Камера Царя» имеют радиусы вписанной окружности (выраженные в единице «Метр»), значения которых имеют непосредственное отношение к константе золотого сечения (1.618…м≡√2.618…; 2.618.. м≡1,618…2) (рисунок 4; таблица 4);
- Параметры Камеры Царя выраженные в единице длины «Королевский кубит» и «Ф2» (0,523606…м=Ф2/5) имеют большое количество значений, которые можно выразить (одновременно с предложенной мерой) посредством целочисленного значения квадратного корня из значений рассчитанных в единице «Королевский кубит» и кратных числу «5» (таблицы 5 и 6). В таблицах 3, 4, 5, 6 подобные значения выделены полужирным шрифтом.
На основании приведенных выше примеров нахождения мер длины кратных мере «Королевский кубит» и на основании полученных результатов анализа значений параметров прямоугольных треугольников (таблицы 3, 4, 5, 6) параллелепипеда помещения «Камеры Царя» (рисунок 4) можно резюмировать:
– мера длины «Королевский кубит» в численном выражении стала таковой по отношению к мере «Метр» и получила таким образом значение иррационального числа (Ф2/5) 0,5236067977499784…;
– на основании единицы меры длины «Королевский кубит» с высокой долей вероятности было спроектировано (в частности) помещение пирамиды «Камера Царя» пирамиды Хуфу;
– посредством универсального языка формальной логики, геометрии, математики (по результатам анализа линейных размеров помещения «Камера Царя») строители пирамиды Хуфу показали свое знание мер длины «Метр» и производной от нее меры – «Королевский кубит» – 0,523606… м или 1/5 от 2,61803… м или 1 м*Ф2. Способ, которым это знание показано, состоит в существовании тождества, которое единственным образомможет быть представлено в виде равенства значений площади треугольника (образованного шириной и длиной помещения пирамиды «камера Царя» и выраженное в единице длины «Метр») и периметра этого же треугольника в тех же единицах длины (27.416…м). При этом, значение числа 27.416… тождества в точности равно квадрату числа 0,523606… меры «Королевский кубит» умноженное на 10 (27.416…м = 5,23606…2).
Поскольку мы пришли к гипотезе о владении строителями пирамид двумя мерами длины – «Королевский кубит» и «Метр» (в современном его значении!) – то мы вправе задавать и следующий вопрос: почему в качестве единицы длины была избрана для нужд строительства именно единица «Королевский кубит» (а не «Метр») имеющая иррациональное значение числа? С точки зрения удобства использования в строительном деле, где требуются различного рода расчеты, подобное использование иррационального числа меры длины приведет неизбежно к трудностям в расчетах. Но, все же ей пользовались! Ответ на данный вопрос может лежать в плоскости предположений о некоторых определенных способах счета, а именно – о системах счисления имеющих иррациональное основание. Безусловно, для многочисленных и сложных расчетов в единицах иррационального числа требовалось некое аппаратное техническое средство – «думалка» – аналог современного компьютера. Разумеется, для каждого технического устройства осуществляющего математические операции требуется наличие алгоритмической системы, на основе которой и осуществляются эти математические операции. В таком случае наиболее рациональным подходом к решению поставленных задач расчетов в единицах иррационального числа при строительстве представляется подход с использование систем счисления имеющих иррациональное основание. Рассмотрим эту версию более подробно относительно существующих сегодня систем счисления с иррациональным основанием.
2. Позиционная система счисления с иррациональным основанием
В чем же состоит существенное преимущество систем счисления с иррациональным основанием по отношению к системам счисления имеющим основание целое число?
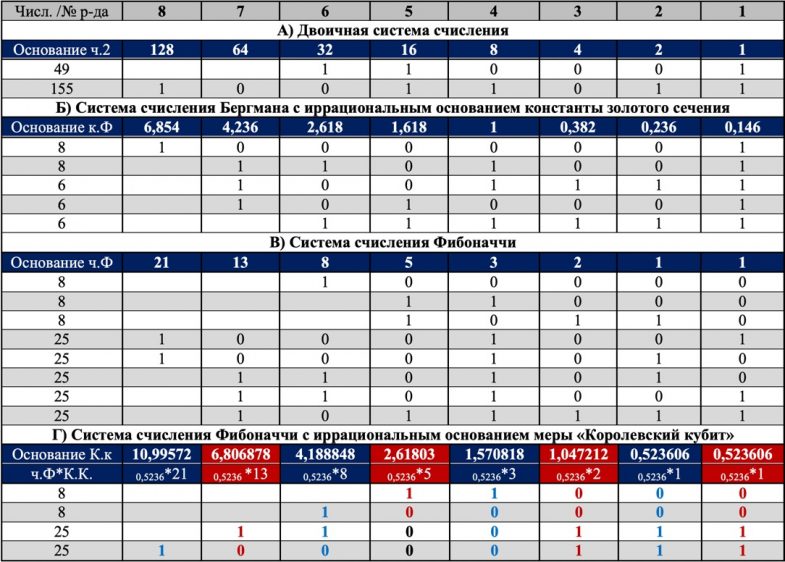
Наиболее часто употребляемыми позиционными системами являются: двоичная (в дискретной математике, информатике, программировании); троичная; восьмеричная; десятичная (используется повсеместно); двенадцатеричная (счёт дюжинами); шестнадцатеричная (используется в программировании, информатике); двадцатеричная; шестидесятеричная (единицы измерения времени, измерение углов и, в частности, координат, долготы и широты). Сегодня двоичная система используется практически во всех современных компьютерах и прочих вычислительных электронных устройствах. Двоичный код – это способ представления данных в виде кода, в котором каждый разряд принимает одно из двух возможных значений, обычно обозначаемых цифрами 0 и 1. Двоичный код может быть непозиционным и позиционным. Позиционный двоичный код лежит в основе двоичной системы счисления – системы счисления с основанием 2 (таблица 7, А).
Кроме того существует так называемая Фибоначчиева система счисления – смешанная система счисления для целых чисел на основе чисел Фибоначчи (таблица 7, В). В основе лежит теорема Цекендорфа (любое неотрицательное целое число единственным образом представимо в виде суммы некоторого набора чисел Фибоначчи с индексами больше единицы, не содержащего пар соседних чисел Фибоначчи). На основе фибоначчиевой системы счисления строится код (кодирование) Фибоначчи – универсальный код для натуральных чисел, использующий последовательности битов. Комбинация «11» запрещена в фибоначчиевой системе счисления и её используют как маркер конца записи.
Доктор технических наук, профессор А.П. Стахов (разработал компьютерную арифметику Фибоначчи [10] и выдвинул концепцию «компьютеров Фибоначчи» в середине 70-х годов прошлого века [5, 6, 7, 8]) говоря о недостатках существующей сегодня двоичной системы счисления, указывает на значимую для систем счисления проблему: « «Троянским конем» двоичной системы, используемой в микропроцессорах, является ее нулевая избыточность, что не позволяет осуществлять контроль преобразований информации в микропроцессоре». « … Отсутствие избыточности означает, что все двоичные кодовые комбинации в рамках двоичной системы являются «разрешенными», что делает невозможным обнаружение каких-либо ошибок, которые неизбежно (с большей или меньшей вероятностью) могут возникнуть в элементах электронных систем под влиянием различных внешних и внутренних факторов (радиация, электромагнитные воздействия, помехи в шинах питания и т. д.). В наноэлектронике эта проблема становится еще более острой». « …Человечество становится заложником классической двоичной системы счисления, которая лежит в основе современных микропроцессоров и информационных технологий. Поэтому дальнейшее развитие микропроцессорной техники и основанной на ней информационной технологии на основе классической двоичной системы счисления следует признать тупиковым направлением… Необходимо отказаться от классической двоичной системы счисления как информационной и арифметической основы специализированных компьютерных систем и наноэлектронных систем и перейти при их проектировании на новые избыточные системы счисления, сохраняющие все известные преимущества классической двоичной системы счисления (позиционность представления чисел, простота арифметических правил, использование двух {0,1} цифр для представления чисел, простые правила сравнения и округления чисел и др.) и позволяющие улучшить надежность, контролеспособность, помехоустойчивость компьютерных систем и тем самым повысить информационную надежность компьютеров» [9].
В отличие от кода классической двоичной системы код Фибоначчи является избыточным кодом. При этом его избыточность проявляет себя в свойстве многозначности представления натуральных чисел. Подобным свойством многозначности представления чисел обладает так же и первая в истории науки позиционная система счисления Джорджа Бергмана с иррациональным основанием [12], в основании которой лежит константа золотой пропорции (таблица 7, Б).
Таблица 7 – Сравнительное представление разрядов и избыточности кодов различных систем счисления: двоичной, Бергмана с иррациональным основанием константы золотого сечения, Фибоначчиевой, Фибоначчиевой с иррациональным основанием меры «Королевский кубит»
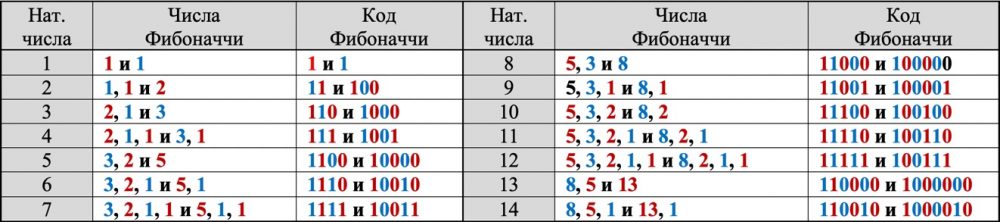
На основе системы счисления Фибоначчи нами создана Фибоначчиевая система счисления с иррациональным основанием меры «Королевский кубит» (таблица 7, Г). В отличие от первой (таблица 7, В), основанием новой системы счислением служит значение числа Фибоначчи умноженное на число меры «Королевский кубит» – 0,52606… . Таким образом, производная от системы счисления Фибоначчи – позиционная система с иррациональным основанием «Королевский кубит». В отличие от Фибоначчиевой системы счисления со свойством различной избыточности кода для представления чисел, позиционная система с иррациональным основанием «Королевский кубит» обладает вполне определенной избыточностью кода: число можно представить двумя (и только двумя) вариантами кодов в связи с введенным нами правилом запрещенных комбинаций кода (таблица 8). Например, число «8» можно представить только двумя кодами 11000 и 100000, а число 7 – 1111 и 10011 и так далее (таблица 9).
Таблица 8 – Запрещенные комбинации кода (с последовательным нечетным количеством знаков «0») в системах счисления на основе Фибоначчиевой
Таблица 9 – Натуральные числа, двояко представленные числами и кодом Фибоначчи
В основе предлагаемого нами правила для системы счисления лежит представление о числах как об идеальных объектах, к которым применимы законы диалектики. Как мы соотносим диалектические закономерности к материальным объектам, так, соответственно, мы соотносим эти законы и к выделенным объектам-идеям. Поэтому числовые значения рекуррентного ряда Фибоначчи нами рассматриваются как подобные идеальные объекты, где можно выделить среди их множества противоположности, которые имеют известное свойство к согласованию. Подобные мысли перекликаются с представлением Пифагора о мужских и женских числах натурального ряда: четные числа Пифагор считал женскими, а нечетные – мужскими. Например, числа 2 и 3 (2+3=5). В рекуррентном ряду Фибоначчи числа 2 и 3 представляют друг по отношению к другу противоположности. В свою очередь – число 5 противоположность числу 3. Таким образом, нами обосновано правило согласования чисел рекуррентного ряда Фибоначчи и сформулировано правило для систем счисления, где основанием является рекуррентный ряд Фибоначчи или производные от этой системы иные системы счисления: «Не могут быть между собой согласованы (позиционно представлены) числа с четными позициями в рекуррентном ряду Фибоначчи или же числа с не четными позициями в этом ряду». Таким образом, «в позиционной системе счисления не возможны комбинации кода с последовательным нечетным количеством знаков «0» ». Позиционную систему счисления на основе сформулированного нами правила (несогласования чисел с четными позициями в рекуррентном ряду Фибоначчи или же чисел с не четными позициями в этом ряду) мы условно назвали Фибоначчиевой системой счисления с диалектическим алгоритмом представления чисел (в отличие от так называемого «жадного» алгоритма представления чисел имеющейся Фибоначчиевой системы счисления, который отличается минимальной формой представления числа в двоичном коде – с наименьшим числом единиц). «Диалектический» алгоритм представления чисел (и соответствующие коды) разработан в связи поиском оптимальной системы счисления на основе Фибоначчиевой (Рисунки 5, 6) .
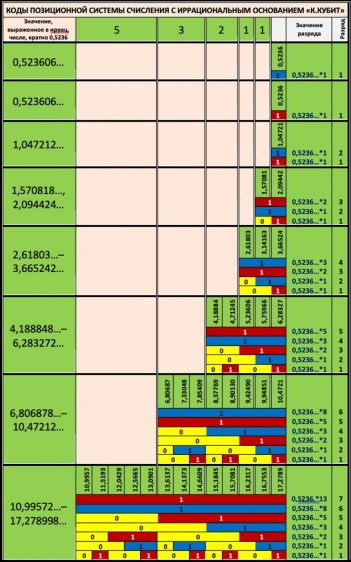
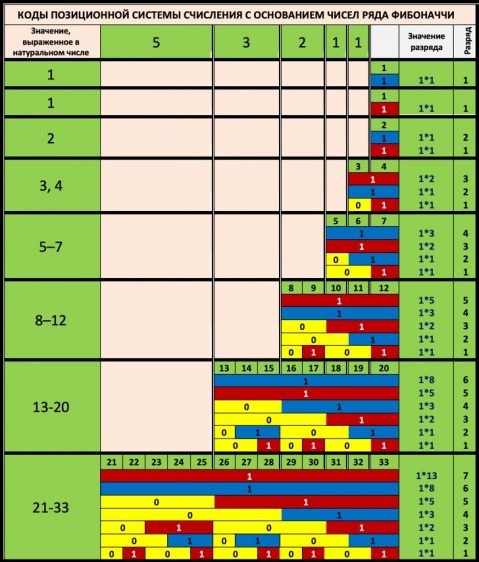 Рисунок 5 – Коды позиционной системы счисления с основанием чисел ряда Фибоначчи
Рисунок 5 – Коды позиционной системы счисления с основанием чисел ряда Фибоначчи
Рисунок 6 – Коды позиционной системы с иррациональным основанием «К. кубит»
Позиционная система с иррациональным основанием (которое выражено в иррациональном числе 0,5236 и кратно Ф2) имеет определенные преимущества перед позиционной системой с целочисленным основанием в:
– надежности системы счисления – ошибка в иррациональном числе не приведет к большим сбоям в системе в сравнении с ошибкой в системе с целочисленными значениями, так как изменение одной из цифр из их множества в иррациональном значении автоматически приведут к обнаружению ошибки из-за «нестыковки» иррациональных чисел. Например, при арифметических операциях с целочисленными значениями, выраженными в единицах «К.к.», изменение одной из цифр не приведет к целочисленному результату операции и, таким образом, автоматически будет обнаружена ошибка;
– удобстве операций – значения позиционной системы с иррациональным основанием 1/5 Ф2 (0,5236…) кратны квадрату золотой пропорции – Ф2 (2,618…) .А это позволяет использовать преимущества десятичной и иных систем счисления с целочисленным основанием – оперировать целочисленными значениями (в данном случае – кратных квадрату золотой пропорции – Ф2) для различных математических операций (деления, умножения…);
– может быть использована (реализована) на основе различных позиционных систем: двоичной, Бергмана, Фибоначчиевой. Для подобной реализации на основе различного рода систем необходимо лишь изменить значение разряда «материнской» системы счисления осуществив операцию умножения существующего разряда на иррациональное значение меры «Королевский кубит».
Обсуждение результатов исследования
Идея о земном «Вояджере» по-своему красива и, безусловно, рациональна. Замысел передачи сообщения посредством земного «Вояджера» безупречно прост: по достижению цивилизацией определенного уровня технологического развития появляется возможность прочесть сообщение, получить необходимые сведения для отправки сообщения и передать сигнал с Земли, воспользовавшись «Вояджером» (комплексом пирамид). По аналогии с нахождением на борту космического «Вояджера» алюминиевой коробки с позолоченным видеодиском с посланием, мы вправе думать о подобном же коробочке с посланием на каком-либо носителе находящейся где-либо в комплексе пирамид Гизы. Но следует понимать, что сегодня, в силу объективных причин (отсутствия технологии дальней космической связи, совершенной системы счисления…), благоразумно не искать послание строителей пирамид или пытаться его раскрыть.
Во-первых, строителями пирамид, вероятно, использовалась система счисления, отличающаяся от современной, – с иррациональным основанием, возможно так же – с основанием чисел Фибоначчи. В этой связи, именно сегодня «прочесть» послание не представляется возможным.
Во-вторых, если этот земной «Вояджер» представляет собой не только устройство доставки послания, но и средство обратной связи – то, не обладая соответствующей технологией связи, весь замысел земного «Вояджера» теряет смысл. И если это так, то строители пирамид наверняка достаточно основательно позаботились о надежном месте для хранения послания (недоступном для варваров, грабителей…), равно как и о возможности осуществления всего замысла проекта земного «Вояджера».
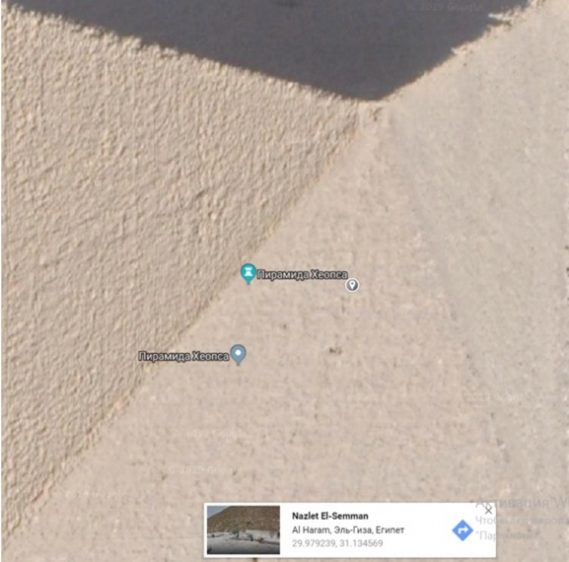
Если говорить о возможном «послании» то наиболее вероятно оно было бы составлено так [2]: важные научные данные цивилизации отражают константы – «π» и «Ф», цивилизации известны: числа Фибоначчи, пифагоровы тройки, значение постоянной тонкой структуры, скорость света (рисунок 7). Цивилизация, оставившая послание, указывает на Пояс Ориона, звезду Альнитак. В качестве «мерной линейки» указаны меры длины «Королевский кубит» (0,5236… м) и «Метр».
Рисунок 7 – Фотографическое изображение пирамиды Хуфу в интернет-сервисе «Google Карты» с отображением географических координат (в интернет-сервисе «Google Карты» можно набрать следующие координаты: 29.9792458 Широты и 31.134417 долготы – координаты Пирамиды Хеопса (Хуфу). Скорость света в метрах за 1 секунду равна 299.792.458)
В замысле земного «Вояджера» обращает на себя внимание то возможное обстоятельство, что, имея возможность «контакта» у развитой цивилизации, право выбора и право первого «шага» к контакту представлено таким образом земной цивилизации. Впрочем, это всего лишь версия, претендующая на обоснованную и логичную в связи с озвученными выше предположениями в рамках версии земного «Вояджера».
По результатам анализа геометрии помещения пирамиды Хуфу «Камера Царя» можно с высокой долей вероятности предположить, что строители пирамиды Хуфу, посредством универсального языка формальной логики, геометрии, математики (по результатам анализа линейных размеров помещения «Камера Царя»), с необходимой полнотой для доказательства показали свое знание мер длины «Метр» и производной от нее меры – «Королевский кубит» – 0,523606… м или 1/5 от 2,61803… м или 1 м*Ф2. Доказательство состоит в существовании тождества, которое единственным образом может быть представлено в виде равенства значений площади треугольника (образованного шириной и длиной помещения пирамиды «камера Царя» и выраженное в единице длины «Метр») и периметра этого же треугольника в тех же единицах длины (27.416…м). При этом значение числа тождества 27.416… в точности равно квадрату числа 0,523606.. меры «Королевский кубит» умноженное на 10 (27.416…м=5,23606…2). Способ, как мы полагаем, которым показано знание двух мер длины (субъективно) изящен и одновременно красив! Если образно представить, то знание о мерах длины строителей пирамид на плато Гизы находилось буквально под ногами каждого входящего в помещение «Камера Царя».
Кроме того было выявлено, что:
– два других прямоугольных треугольника геометрии параллелепипеда помещения «Камера Царя» (см. рисунок 4) имеют радиусы вписанной окружности (выраженные в единице «Метр»), значения которых имеют непосредственное отношение к константе золотого сечения (1.618…м≡√2.618…; 2.618.. м≡1,618…2) (см. таблицу 4);
– диагональ параллелепипеда или гипотенуза треугольника образованного шириной и длиной помещения пирамиды «камера Царя» и выраженное в единице длины «Метр» (в точности 11,70818609426755… м) тождественна значению, получаемому из корня квадратного числа 137,081621618… . Произведение числа равного мере длины «Королевский кубит» (0,5236067977499784…) на 100, а затем – и на значение Ф2 будет тождественно числу 137,081621618… . Полученное число 137,081621618… близко к значению постоянной тонкой структуры (фундаментальной физической постоянной, характеризующей силу электромагнитного взаимодействия) – 137,036….;
– значение периметра треугольника образованного тремя прямыми – гипотенузой боковой поверхности параллелепипеда помещения «Камера Царя», его длиной, и диагональю – тождественно значению, получаемому из корня квадратного 16-го числа Фибоначчи (31.416…м ≡√987).
Таким образом, мы пришли к обоснованной гипотезе: строители пирамиды Хуфу располагали (как минимум) двумя мерами длины и преднамеренно предпочли мере длины «Метр» меру «К.кубит». В чем же состояло значимое преимущество одной меры над другой? В этой связи нами проведено сравнение кодов систем счисления с различными типами основания на примере значений параметров параллелепипеда помещения «Камера Царя» выраженных в единице «Метр». Было выявлено, что на основании систем счисления с иррациональным основанием (предлагаемой Фибоначчиевой позиционной системы счисления с основанием «Королевский кубит», системы счисления Бергмана (таблица 7)) линейные размеры параллелепипеда помещения «Камера Царя» можно выразить комбинацией относительно простого (в сравнении с кодом позиционной системы с основанием «2» и «ч.Ф.») двоичного кода (таблица 10).
Таблица 10 – Сравнительное представление кодов систем счисления с различными типами основания на примере значений параметров параллелепипеда помещения «Камера Царя» выраженных в единице «Метр»
| Параметры | Единица длины «Метр» | Значение в позиционной системе счисления с основанием | ||
| «2» (Бинарная, с рациональн. осн-ем.) | «к.Ф.» (Бергмана, с ирррациональн. осн-ем) | «ч.Ф*К.к.» (Фибоначчиевая+К.к., с ирррациональн. осн-ем) | ||
| Длина | 10,47212… | 11111111101010101100 | 10101000 | 111111
1001111 |
| Ширина | 5,23606… | 1111111110101010110 | 1001000
111000 |
11100
100100 |
| Высота | 5,854… | 1011011011110 | 1010000
1001110 |
√(1110111/1100)*1100 |
Можно представить двоичным кодом параметры помещения «Камера Царя» выраженные так же в целочисленных единицах «Королевский кубит»: длина – 20, ширина – 10, высота – √125. При этом уже наиболее «экономичными» системами счисления будут системы с рациональным основанием – «двоичная» и «Фибоначчиевая». Последняя, в отличие от двоичной системы, еще будет обладать избыточностью кода. Например, длину помещения можно отобразить кодом 101002 и 111111ф (1001111ф), а ширину – 10102 и 11100ф(100100ф).
Таким образом, основным преимуществом использования меры «Королевский кубит» (по отношению к иным мерам длины) является ее специфическая «универсальность» – возможность представления значения в различных системах счисления с рациональными и иррациональными основаниями, множественность представления кода (критерий надежности системы счисления) в каждой из них.
Мера длины «Королевский кубит» в численном выражении стала таковой по отношению к мере «Метр» и получила значение иррационального числа (Ф2/5) 0,5236… . В свою очередь, целочисленная мера длины «Метр» непосредственно связана своим происхождением с мерой времени – секундой и физической переменной – гравитационным ускорением. Закономерно возникает вопрос: совпадением ли, случайностью ли является происхождение меры длины «Королевский кубит»? Во всяком случае: «Если факты противоречат теории, то нужно отбрасывать теорию, а не факты» А.Ю. Скляров.
Заключение
- Полученные результаты анализа геометрии помещения пирамиды Хуфу «Камера Царя» могут быть интерпретированы в рамках версии о предназначении комплекса пирамид Гизы как своеобразного земного «Вояджера» представителей развитой цивилизации.
- «Послание» может быть сформулировано и «прочитано» нами в виде универсального «языка» формальной логики, геометрии и математики.
- Значения системы мер в Древнем Египте кратны по отношению к мере «Локоть царский» (=0,5235 м), а мера длины «Королевский кубит» – используемая при строительстве пирамиды Хуфу – иррациональное число 0,523606… .
- Важным результатом анализа геометрических размеров помещения пирамиды Хуфу «Камера Царя» стало выявление тождества в виде равенства значений площади треугольника (образованного шириной и длиной помещения пирамиды «камера Царя» и выраженное в единице длины «Метр») и периметра этого же треугольника в тех же единицах длины.
- Сформулирована гипотеза о владении строителями пирамид двумя мерами длины «Королевский кубит», «Метр» и существовании некого технического средства с системой счисления с иррациональным основанием.
- Показано, что современные системы счисления имеют существенный недостаток в виде нулевой избыточности кода в отличие от систем счисления с иррациональным основанием.
- На основании Фибоначчиевой системы счисления и меры «Королевский кубит» разработана система счисления с основанием в виде иррационального числа 0,523606… и показана ее оптимальность для операций счисления в одноименных единицах меры длины.
Список литературы:
- Ворон, А.В. Комплекс пирамид Гизы как единое устройство связи // «Академия Тринитаризма», М., Эл № 77-6567, публ.24559, 16.06.2018
- Ворон, А.В. Культорологический и технологический аспект великой пирамиды // «Академия Тринитаризма», М., Эл № 77-6567, публ.24005, 29.11.2017
- Ворон, А.В. Свойства треугольников Кеплера, Фибоначчи и их связь с геометрией пирамиды Хуфу // «Академия Тринитаризма», М., Эл № 77-6567, публ.24320, 04.03.2018
- Ворон, А.В. Способ воспроизведения геометрии пирамиды Хуфу на основе использования чисел Фибоначчи // «Академия Тринитаризма», М., Эл № 77-6567, публ.24204, 20.01.2018
- Стахов, А.П. Избыточные двоичные позиционные системы счисления. В кн. Однородные цифровые вычислительные и интегрирующие структуры, вып.2. Изд-во Таганрогского радиотехнического института, 1974 г.
- Стахов, А.П. «Фибоначчиева» двоичная арифметика и ее применение для контроля вычислительных систем. – В кн. Однородные вычислительные системы и среды. Материалы IV Всесоюзной конференции. Киев, «Наукова думка», 1975.
- Стахов, А.П. Использование естественной избыточности «фибоначчиевых» систем счисления для контроля вычислительных систем. Автоматика и вычислительная техника, №6, 1975 г.
- Стахов, А.П. «Фибоначчиевые» двоичные позиционные системы счисления. В сб. Кодирование и передача дискретных сообщений в системах связи. Москва, Наука, 1976 г.
- Стахов, А.П. Микропроцессоры Фибоначчи – как одна из базисных инноваций будущего технологического уклада, изменяющих уровень информационной безопасности систем // «Академия Тринитаризма», М., Эл № 77-6567, публ.16759, 16.08.2011
- Стахов, А.П. Коды золотой пропорции. – Москва: Радио и связь, 1984. – 152 с.
- Темаров, А. Геометрия Великой пирамиды. https://lah.ru/geometriya-velikoj-piramidy/
- Bergman, G. A number system with an irrational base // Mathematics Magazine, 1957, No 31: 98–119.
















А главного вы так и не увидели! Все много проще. Пи/6=0,5236 – 30 градусов дуги окружности. То есть один знак зодиака. Ну и главное: если умножить высоту пирамиды и периметр основания на 43200, получим полярный радиус Земли длину экватора.
Там по всей пирамиде металлические стержни, их много в большой галереи. Чё вы нееиувидели до сих пор???
Я не сильно вникал, но число Ф (Фидия, Фибоначчи) легче находить не через корень из 5, а через 2cos36 = 1.6180339887498948482045868343656.. – и если начать его возводить в степеня (положительные и отрицательные – т.е. умножать и делить на самоё себя) – очень легко придём к целочисленному ряду, только не Фибоначчи, а Люка, с двоечкой посередине -1, 2, 1, 3, 4, 7, 11, 18, 29 и т.д. Парные степеня Фи (+ и -) суммируются, непарные – вычитаются – и таким чудом из степеней иррационального ряда получаем целочисленный. Есть формула Бинэ, по которой делением на корень из 5 можно получить и целочисленный ряд Фибоначчи – там наоборот парные степени Фи вычитаются, непарные слагаются.. Но сам иррациональный ряд “Фи в степени эн” обладает множеством удивительных свойств.. Во-первых ему всё равно: прибавлять к меньшему большее или умножать на Фи.. И во-вторых, многие из выше упомянутых чисел – узнаваемы, как члены этого ряда, только со сдвинутой запятой.
Интереснр, как вы менно вы так просто переводили иррациональное десятичное число в бинарную систему исчисления (с рац. осн) в таблице 10 ?.
Если бы мы не использовали метрическую систему, то мы не смоглти бы расшифровать приведенные закономерности ? Как создатели пирамид были уверены, что у нас будем именно метрическая система ? Нет никакой гарантити от того, что например после 3й мировой войны, мы будем использовть английскую систему, например с дюймами, а метрическая со временем забудется, тогда и соотношение на пирамиде не будет иметь смысла.
Ivan писал: Если бы мы не использовали метрическую систему, то мы не смогли бы расшифровать приведенные закономерности ?
Если бы мы не использовали метрическую систему мы не поняли бы, что скорость света численно совпадает с широтой Великой Пирамиды с точностью до девятого знака.
Стоп, стоп, стоп, братцы! Девятый знак после запятой по широте – это 100 (сто) микрон. Кто это, интересно, мерял с такой точностью? Ссылочку не приведете?
Так всем интересно! Это, как раз, и есть главный вопрос!
Только, конечно в этом случае не о микронах речь. Разделите половину длины меридиана на миллиард. Это и будет реальная точность позиционирования.
Почему никто до сих пор не удосужился поместить в эту точку памятную капсулу со всеми необходимыми современными описаниями?!
Я не большой поклонник всех этих игрищ с числами вокруг пирамид (особенно Хуфу), но для предполагаемой развитой цивилизации гораздо естественнее взять расстояние от экватора до полюса по меридиану а не длину руки родившегося через тысячелетия короля Генриха 1-го за основу меры длины.
Не указан источник данных из таблицы 1: Таблица 1 – Система мер длины в Древнем Египте (с V по I век до нашей эры). Мысль о связи чисел Фибоначчи с геометрией Пирамид не нова. На мой взгляд, учитывая недостаточность открытых данных по комплексу физических, биологических, астрономических, географических, алгоритмических, исторических и проч. междисциплинарных исследований “Единственного Чуда Света”, специалисту Кафедры легкой атлетики следовало бы говорить о Великой Пирамиде как об устройстве связи с современностью в этом физкультурном, а не космическом аспекте. Говорить, например, на предмет организации Международных легкоатлетических соревнований – забегу вокруг Пирамид, или тяжелоатлетических соревнований – командному замесу известняковых блоков и их перемещению к местам многочисленных дефектов, образовавшихся за последние столетия. Результаты соревнований с соответствующим музыкальным сопровождением следовало бы при этом попытаться транслировать через “вентканалы” многочисленным болельщикам, которых можно рассадить по “ступеням” Пирамид. Вот это и было бы для начала испытание “устройства связи” не на словах, а на деле…
Фу! Грубо и пошло…
Оставляя “устройство связи” на совести автора, стоит отметить, что связь с рядом Фибоначчи и золотым сечением отнюдь не кажется лишенной смысла.
Спорт и музыка – это большое дело, а не грубость. К тому же это понятно абсолютно всем.
А по сути вопроса есть ли замечания? Или только к легкой атлетике?
Илья спрашивал: А по сути вопроса есть ли замечания? Или только к легкой атлетике?
Можно пройтись по абзацам, но мы даже с легкой атлетикой не справляемся… А еще есть тяжелая атлетика и тд.!