Аннотация. Исследованы два варианта геометрии многогранника Дюрера – условно названные как «традиционный» и «альтернативный». Выявлены геометрические свойства обеих вариантов многогранников. По результатам натурного эксперимента выявлено, что «альтернативный» вариант многогранника обладает свойством комплементарности.

Ключевые слова: многогранник Дюрера, симметричный объект, трехмерная модель, геометрический объект.

Введение. Многогранник Дюрера – многогранник, изображённый на гравюре Альбрехта Дюрера «Меланхолия §I» (рисунок 1). Массивный многогранник расположен у основания лестницы и доминирует в левой половине гравюры. Точная геометрия этого тела сегодня является предметом незаконченных научных споров.

Основная часть. Нами исследованы два варианта геометрии многогранника Дюрера. Один (условно названный нами «традиционный» [5]) – с геометрическими параметрами шести больших граней: длина большей стороны грани соотносится к меньшей в отношении квадрата золотой пропорции (1), а средняя к меньшей – в отношении золотой пропорции (2). Большая и меньшая стороны рассматриваемой фигуры образуют между собой угол в 108°, а большие стороны – в 72° (рисунок 2, слева). Кроме того, установлены так же следующие равенства для «традиционного» многогранника Дюрера ((3), (4)). Предлагаемый нами многогранник – «альтернативный» – имеет геометрию больших шести граней, которую характеризуют равенства (5) и (6). Он может быть построен из четырех треугольников Фибоначчи – когда два больших треугольника соединены между собой большими катетами, а два других – меньших – прилегают своими гипотенузами к меньшим катетам больших треугольников Фибоначчи (рисунок 2, справа). (Треугольник Фибоначчи – прямоугольный треугольник с соотношением катетов равным золотой пропорции [1, 2, 3, 4]). Большая и меньшая стороны грани «альтернативного» многогранника образуют между собой угол ≈63,435…° Таким образом, получена геометрическая фигура, обладающая следующими свойствами (5), (6).

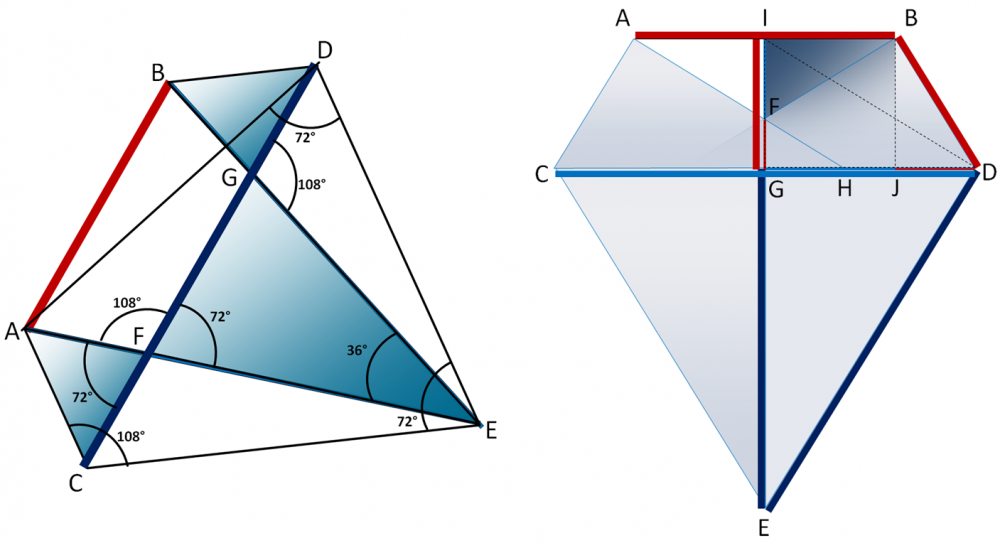
FD/CF=FE/AF=АD/AC=1,61803…²                                                          (1)

FG/CF=CD/АB=1,61803…                                                                          (2)

АD=CE=DE                                                                                                 (3)

CD=AE=BE                                                                                                 (4)

CD/AB=AH/CA=IF/FG=FH/FG=EG/GD=GJ/JD=BJ/JD=1,61803…        (5)

ED/DB=EG/GI=1,61803…²                                                                         (6)

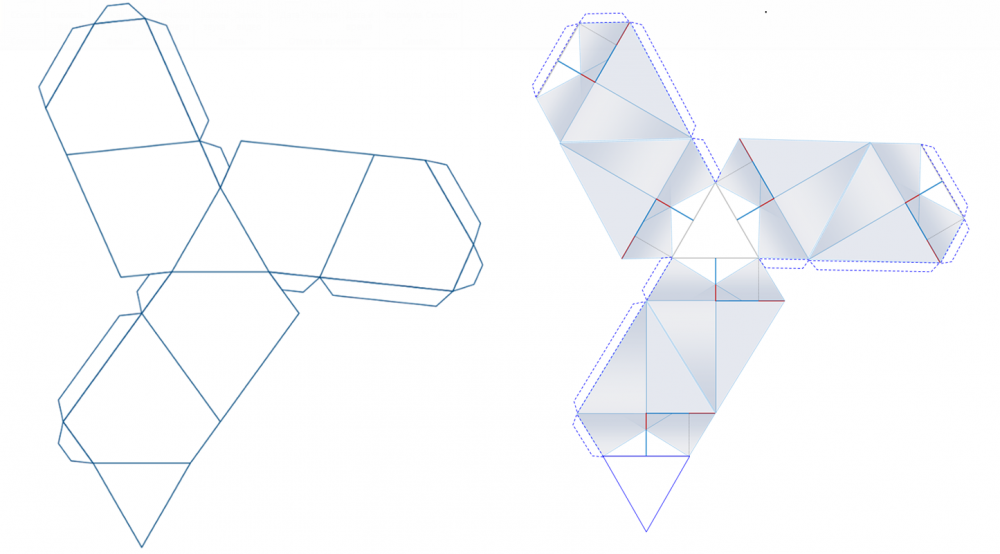
Для изготовления трехмерных моделей двух вариантов представления многогранника Дюрера были рассчитаны и расчерчены две развертки (рисунок 3). На их основе были изготовлены трехмерные натурные модели двух многогранников Дюрера (рисунок 4).

По результатам натурного эксперимента выявлено, что «альтернативный» вариант представления многогранника Дюрера обладает свойством комплементарности – многогранники образуют разнообразные составные геометрические объекты (как не симметричные, так и симметричные (рисунок 5, 6, 7, 8). Внутреннее пространство – полость – одной из составных моделей, образованное треугольными гранями двадцати «альтернативных» многогранников, имеет форму икосаэдра (рисунок 8).

Заключение.

1. Исследованы два варианта геометрии многогранника Дюрера – условно названные как «традиционный» и «альтернативный».
2. Выявлены геометрические свойства обеих вариантов многогранников.
3. По результатам натурного эксперимента выявлено, что «альтернативный» вариант многогранника обладает свойством комплементарности.

Список литературы:

1. Ворон, А.В. Геометрический треугольник Фибоначчи и пирамида Хеопса // «Академия Тринитаризма», М., Эл № 77-6567, публ.23546, 13.07.2017.
2. Ворон, А.В. Дуальность и комплементарность треугольников Кеплера, Фибоначчи и их связь с геометрией платоновых тел // «Академия Тринитаризма», М., Эл № 77-6567, публ.24401, 06.04.2018.
3. Ворон, А.В. Культорологический и технологический аспект великой пирамиды // «Академия Тринитаризма», М., Эл № 77-6567, публ.24005, 29.11.2017.
4. Ворон, А.В. Свойства треугольников Кеплера, Фибоначчи и их связь с геометрией пирамиды Хуфу // «Академия Тринитаризма», М., Эл № 77-6567, публ.24320, 04.03.2018.
5. https://www.jacquier.org/Art_contemporain/Yvo_Jacquier-Construction_Polyedre_Durer-3.pdf