«…Из двух названных раньше треугольников равнобедренный получил в удел одну природу, тогда как неравнобедренный – бесчисленное их множество. Из этого множества нам должно избрать наилучшее… Что ж, если кто-нибудь выберет и назовет нечто еще более прекрасное … мы подчинимся ему не как неприятелю, но как другу».

Платон, «Тимей»

«…Надо сомневаться и проверять».

А. Ю. Скляров

В одном из своих самых знаменитых произведений «Тимей» [6] Платон развивает «атомистическое» учение. В качестве «первоатомов» Платон принимает треугольники двух видов – прямоугольный равнобедренный и прямоугольный с меньшим катетом, равным половине гипотенузы, квадрат которой в три раза больше квадрата этого катета. Согласно описанию Платона в «Тимей» [6] четыре равнобедренных треугольника, сложенные в квадрат образуют сложный «атом». Из подобных квадратов можно сложить куб. Шесть других фигур сложенных в равносторонний треугольник образуют грань, из которой, в свою очередь, можно построить три правильных многогранника: тетраэдр (4 грани), октаэдр (8 граней) и икосаэдр (20 граней). Интерпретировав слова Платона приведенные нами в эпиграфе нашей статьи как не случайную оговорку, а как представленную возможность альтернативного способа построения тетраэдра, октаэдра, куба и икосаэдра на основе иных треугольников (отличных от двух видов, описанных Платоном в «Тимей»), мы сделали попытку построения геометрии платоновых тел посредством двух треугольников – Кеплера и Фибоначчи [3, 4, 5]. Для достижения поставленной цели исследования мы использовали натурное трехмерное моделирование геометрических тел-моделей составленных из треугольников Кеплера и Фибоначчи, а так же – геометрическое построение плоских фигур.

Платон сообщает в «Тимей»: «…Огонь и земля, вода и воздух суть тела, а всякое тело имеет глубину. Между тем любая глубина по необходимости должна быть ограничена некоторыми поверхностями; притом всякая прямолинейная поверхность состоит из треугольников. Однако все вообще треугольники восходят к двум, из которых каждый имеет по одному прямому углу и по два острых, но при этом у одного по обе стороны от прямого угла лежат равные углы величиной в одну и ту же долю прямого угла, ограниченные равными сторонами, а у другого – неравные углы, ограниченные неравными сторонами. … между множеством треугольников есть один, прекраснейший, ради которого мы оставим все прочие, а именно тот, который в соединении с подобным ему образует третий треугольник – равносторонний. …нам приходится отдать предпочтение двум треугольникам как таким, из которых составлено тело огня и [трех]прочих тел: один из них равнобедренный, а другой таков, что в нем квадрат большой стороны в три раза больше квадрата меньшой. …четыре рода действительно рождаются из выбранных нами треугольников: три рода слагаются из одного и того же неравнобедренного треугольника [тетраэдр, октаэдр, икосаэдр] и только четвертый род [куб] – из равнобедренного. …В запасе оставалось еще пятое многогранное построение, его Бог определил для Вселенной и прибегнул к нему в качестве образца»[6].

Согласно представленному Платоном описанию двух видов (условно так определим и будем в дальнейшем их так называть) треугольников мы их наглядно отобразили в рисунке 1. Отношение большего катета к меньшему катету первого вида треугольника равно 1,732050807568877.

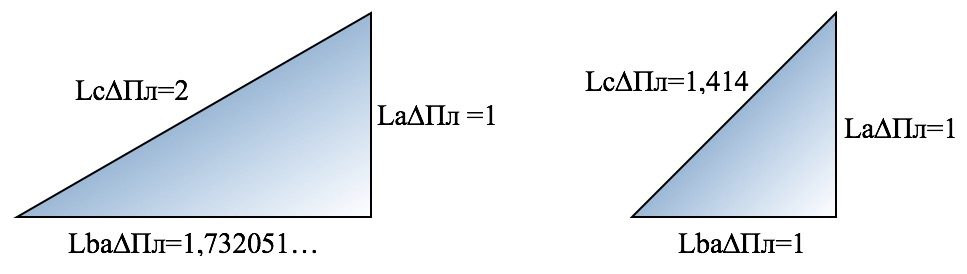
Описывая построение четырех тел, Платон сообщает о нахождении треугольников в первом из них: «…его первоначало – треугольник, у которого гипотенуза вдвое длиннее меньшего катета. Если такие треугольники сложить, совмещая их гипотенузы, и повторить такое действие трижды, притом так, чтобы меньшие катеты и гипотенузы сошлись в одной точке как в своем центре, то из шестикратного числа треугольников будет рожден один, и он будет равносторонним. Когда же четыре равносторонних треугольника окажутся соединенными в три двугранных угла, они образуют один объемный угол, а именно такой, который занимает место вслед за самым тупым из плоских углов. Завершив построение четырех таких углов, мы получаем первый объемный вид, имеющий свойство делить всю описанную около него сферу на равные и подобные части» [6].

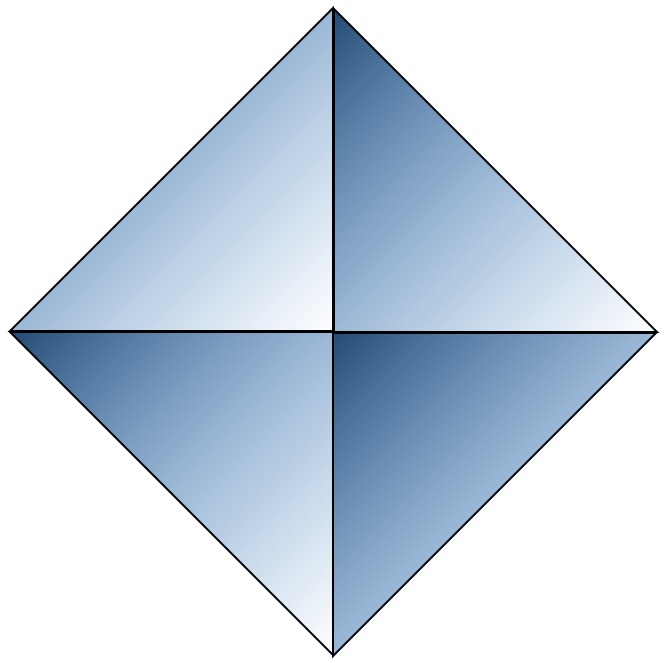
Исходя из описания Платона о составляющих граней тетраэдра, мы построили равносторонний треугольник из 6-ти треугольников первого вида (рисунок 2).

Далее Платон сообщает об относительно легком для представления способе построения из первого вида треугольника второго и третьего тела: «…Второй вид [октаэдр]строится из таких же исходных треугольников, соединившихся в восемь равносторонних треугольников и образующих каждый раз из четырех плоских углов по одному объемному; когда таких объемных углов шесть, второе тело получает завершенность. Третий вид [икосаэдр]образуется из сложения ста двадцати исходных треугольников и двенадцати объемных углов, каждый из которых охвачен пятью равносторонними треугольными плоскостями, так что все тело имеет двадцать граней, являющих собой равносторонние треугольники» [6].

Для построения куба Платон избрал второй вид треугольников – равнобедренный. В «Тимей» о построении куба сказано: «…равнобедренный треугольник породил природу четвертого [вида], и притом так, что четыре треугольника, прямые углы которых встречались в одном центре, образовывали квадрат; а из сложения шести квадратов возникало восемь объемных углов, каждый из с которых гармонично охватывается тремя плоскими прямыми углами. Составившееся таким образом тело имело очертания куба, наделенного шестью квадратными плоскими гранями»[6]. Согласно описанию мы построили из треугольников второго вида одну из шести граней куба (рисунок 3).

Приняв и интерпретировав слова Платона, приведенные нами в эпиграфе нашей публикации, как возможность альтернативного способа построения тетраэдра, октаэдра, куба и икосаэдра на основе иных треугольников, мы, в рамках и продолжая тему связи треугольников Кеплера и Фибоначчи [3, 4, 5], поставили две задачи нашего исследования:

– обосновать дуальность и комплементарность треугольников Кеплера и Фибоначчи;

– показать возможность построения геометрии платоновых тел посредством двух треугольников – Кеплера и Фибоначчи и возможность вписать эти тела в додекаэдр.

Для решения первой задачи мы использовали натурное трехмерное моделирование геометрических тел-моделей составленных из треугольников Кеплера и Фибоначчи, а для решения второй – геометрическое двухмерное плоскостное построение или, иначе говоря, геометрическое построение плоских фигур.

Разрешая первую задачу, мы выявили в двухмерном пространстве взаимосвязь геометрии 2-х треугольников – Кеплера и Фибоначчи (рисунок 1):

– при взаимном расположении треугольников Кеплера и Фибоначчи в положении, когда они соприкасаются зеркально равными гипотенузами – можно вписать третий треугольник – треугольник Кеплера (в образовавшийся неправильный четырехугольник), который соединяет гипотенузой прямые углы двух других треугольников (рисунок 3);

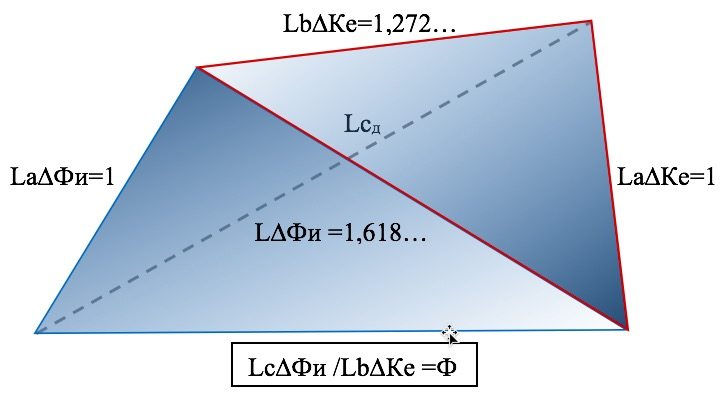
– отношение меньшего катета к гипотенузе треугольника Кеплера равно отношению большего катета к меньшему треугольника Фибоначчи (значение отношений названых сторон двух треугольников равно константе Ф) (рисунок 4);

– равенство меньших катетов треугольников Кеплера и Фибоначчи при равенстве большего катета треугольника Фибоначчи и гипотенузы треугольника Кеплера (рисунок 4).

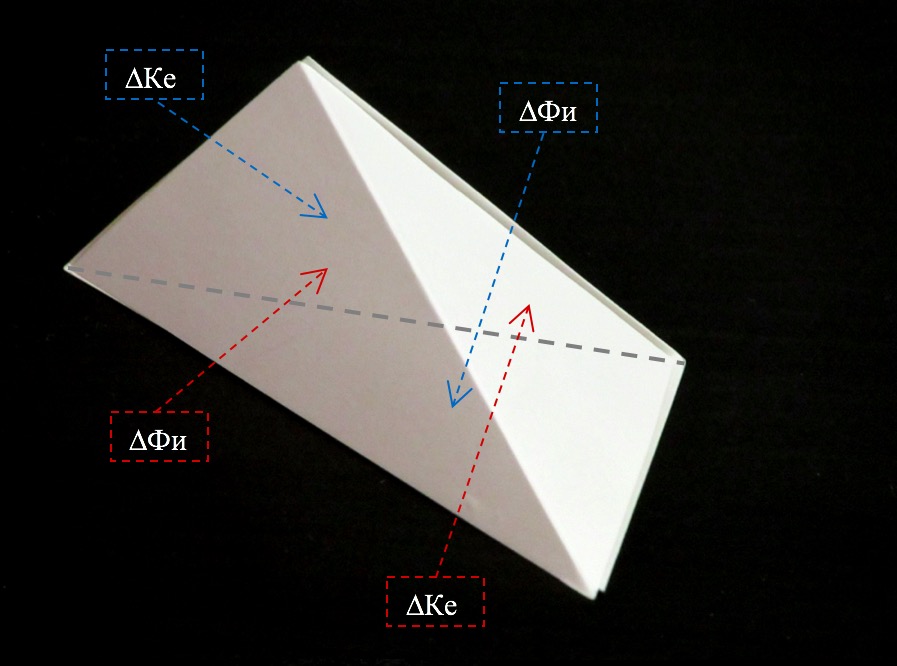
Для обоснования комплементарности двух рассматриваемых нами треугольников мы построили натурную геометрическую объемную модель, состоящую из 2-х пар треугольников (рисунок 5). Эта модель показывает способ построения геометрического тела, при котором являются общими для названных двух пар треугольников гипотенуза треугольника Кеплера и больший катет треугольника Фибоначчи. Пары объединены в единое целое – объемное геометрическое тело – посредством общих больших катетов треугольников Кеплера и гипотенуз треугольников Фибоначчи.

Взаимодополняемость треугольников Кеплера и Фибоначчи прослеживается и при построении геометрической объемной модели, включающей три пары треугольников (рисунок 6). Пары треугольников (как и в предыдущей модели – у которых являются общими гипотенуза треугольника Кеплера и больший катет треугольника Фибоначчи) при этом способе расположены по отношению друг к другу под углом в виде равностороннего треугольника, ребра которого образованы гипотенузами треугольника Фибоначчи. Непосредственно с рассматриваемыми ребрами равностороннего треугольника соприкасаются меньшие катеты трех треугольников Кеплера. Следует отметить, что больший катет треугольника Кеплера не пересекается в средней его части с подобными катетами треугольников Кеплера других двух пар (на рисунке 6 – пересекается).

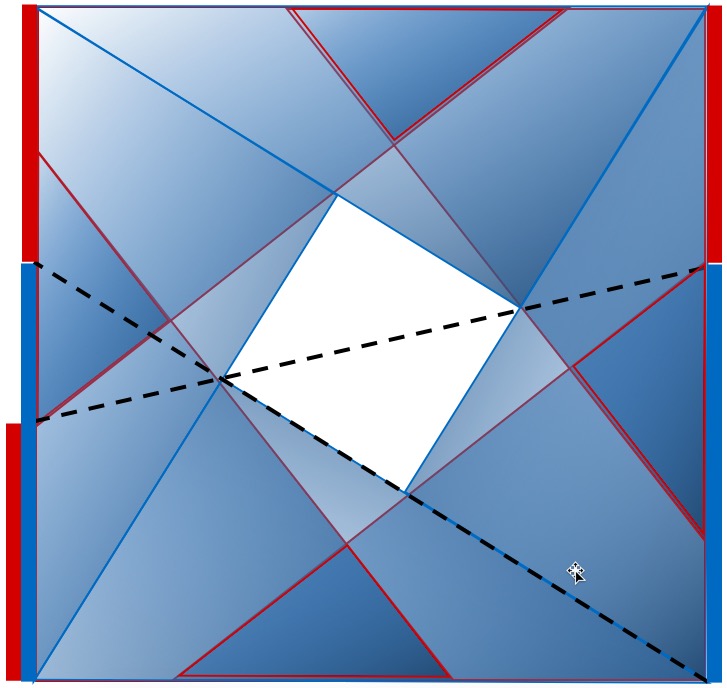
Продолжая геометрическое двухмерное плоскостное построение (геометрическое построение плоских фигур) мы вписали в квадрат показанными в рисунке 7 способами по четыре треугольника Кеплера и Фибоначчи с равными диагоналями. При первом способе прямые углы треугольника Кеплера являются углами квадрата. Между собою четыре треугольника Фибоначчи так же вписанные в квадрат уже другим способом соприкасаются между собой меньшим и большим катетами, а их гипотенузы образуют периметр квадрата. Общая для двух треугольников точка пересечения находится в основании прямого угла треугольника Фибоначчи. По краям квадрата нами обозначены красным и синим цветом пропорциональные Золотому сечению отрезки.

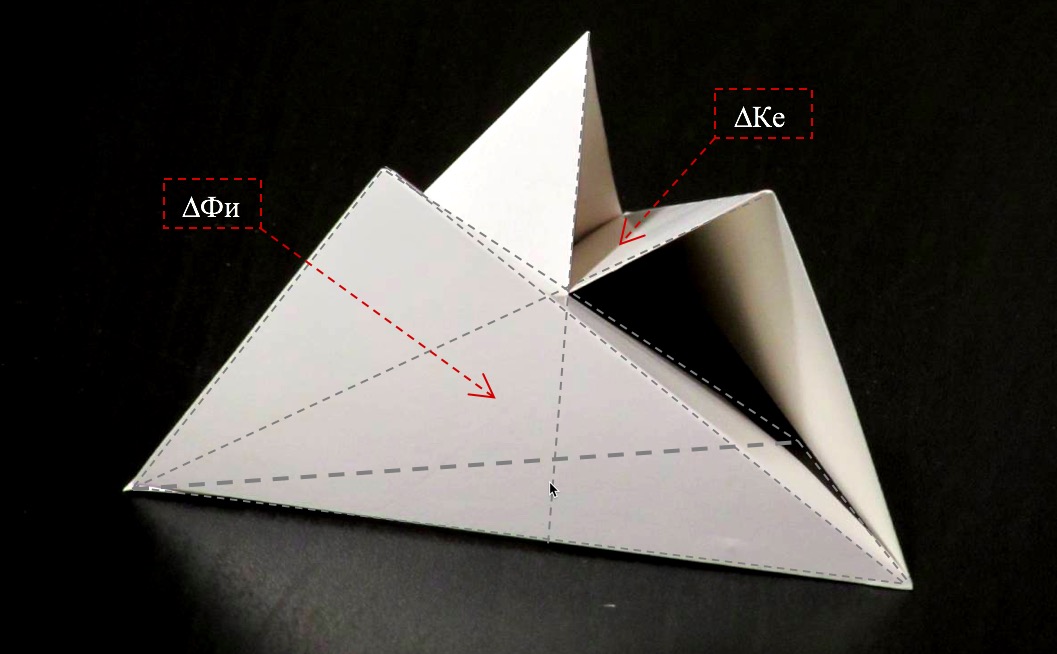
Дуальность и комплементарность треугольников Кеплера и Фибоначчи можно проследить и в модели неправильного тетраэдра, три ребра которого и вершины образованы тремя треугольниками Кеплера (рисунок 8). Три боковые поверхности этого треугольника можно без погрешностей составить из шести других треугольников – с линейными размерами треугольника Фибоначчи (по два на каждую сторону и в положении, при котором общим для двух треугольников является больший катет).

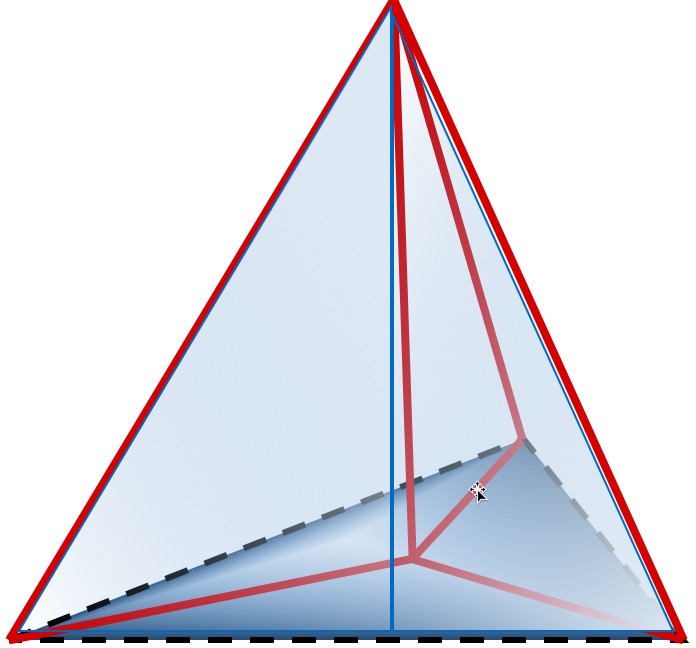
Основание рассматриваемого нами неправильного тетраэдра образовано меньшими катетами шести треугольников Фибоначчи и является равносторонним треугольником.

Приступая к решению второй задачи нашего исследования (показать возможность построения геометрии платоновых тел посредством двух треугольников – Кеплера и Фибоначчи) мы оговоримся о некоторых обозначенных нами ограничивающих условиях (о назначении которых станет понятно в завершающей части статьи):

– построение геометрических тел (платоновых тел) допускается треугольниками Кеплера и Фибоначчи различных размеров, но не более трех;

– количество треугольников разных видов должно быть одинаково (парно представлено в геометрии тел по количеству и их размерам);

– треугольники Кеплера и Фибоначчи должны образовывать центр симметрии построенного геометрического тела;

– треугольники Кеплера и Фибоначчи должны позволять формировать структурообразующие элементы тела: его вершины, грани и центр симметрии.

Перечисленные условия позволили нам построить четыре геометрических тела (неправильные тетраэдр и октаэдр, куб, икосаэдр) и вписать их додекаэдр.

Построение неправильного тетраэдра. Для построения неправильного тетраэдра нами использовано шесть пар треугольников Кеплера (на рисунке 9 обозначены красным цветом) и Фибоначчи (на рис. 9 обозначены синим цветом) разных размеров (по три больших и три малых треугольников Кеплера и столько же больших и малых треугольников Фибоначчи). Три малых треугольника Кеплера образуют меньшую часть трех ребер тетраэдра своими гипотенузами, и столько же больших треугольников Фибоначчи – большую часть этих ребер и основание геометрического тела. Три малых треугольника Фибоначчи образуют общие катеты: с одной стороны (малым катетом) – с малым катетом треугольника Кеплера, с другой стороны (большим катетом) – с меньшим катетом большего треугольника Фибоначчи. Три больших треугольника Кеплера (на рис. 9 обозначены красными пунктирными линиями) образуют пары с тремя большими треугольниками Фибоначчи как в моделях, у которых являются общими гипотенуза треугольника Кеплера и больший катет треугольника Фибоначчи (см. рисунки 5, 6)).

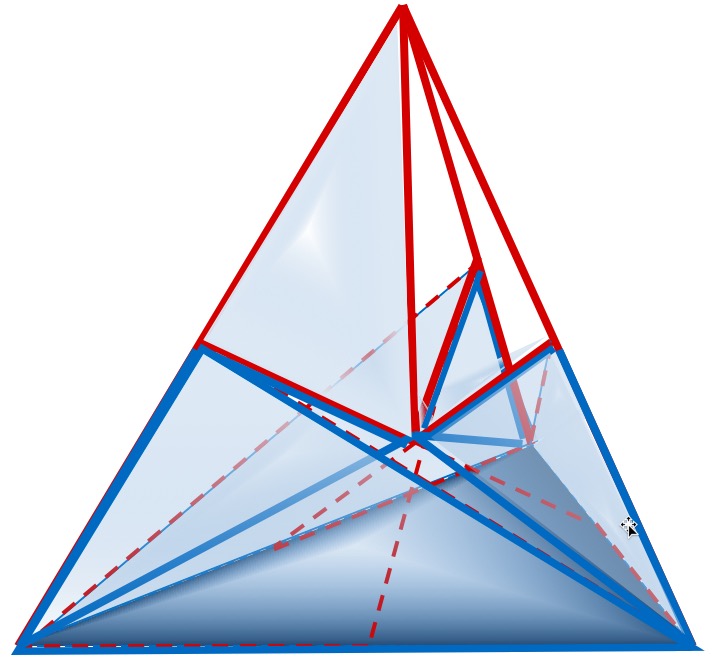
Для наглядного представления относительно сложного построения неправильного тетраэдра нами сделаны рисунки, наглядно представляющие геометрическое тело сверху и его сечение, проходящее через вершину и центр его основания – равносторонний треугольник (рисунок 10, 11).

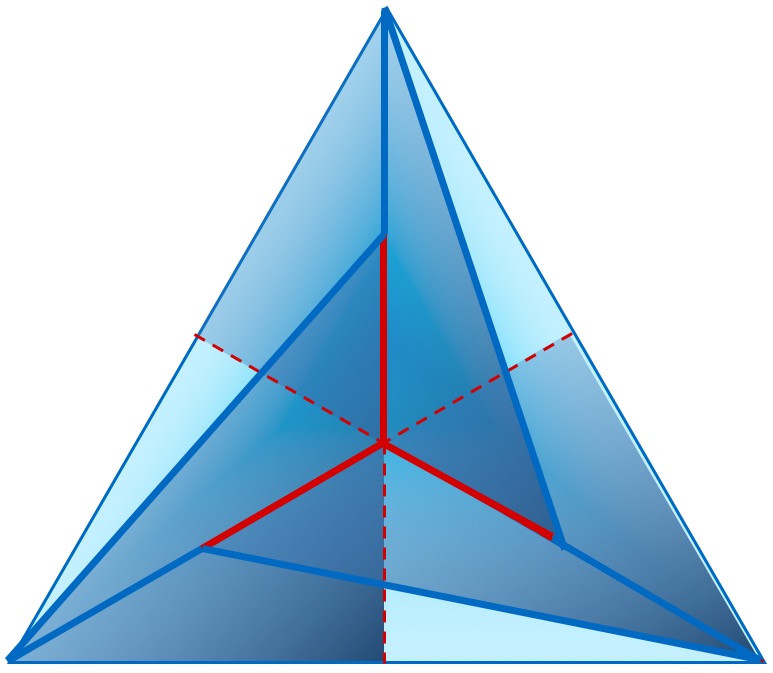
Построение неправильного октаэдра. Для построения неправильного октаэдра необходимо 12 пар треугольников Кеплера и Фибоначчи – равное количество больших и меньших треугольников (рисунок 12). Своеобразный «каркас» геометрического тела формируют восемь больших треугольников Кеплера соприкасающихся между собой большими катетами в вертикальной плоскости и меньшими – в сагиттальной и горизонтальной плоскостях (крест-накрест) (рисунок 13). Восемь треугольников Фибоначчи местами соединения гипотенуз и больших катетов образуют две противолежащих вершины тела, а меньшими своими катетами – периметр и четыре вершины тела. Больший катет больших треугольников Фибоначчи и гипотенузы больших треугольников Кеплера образуют апофемы двух пирамидальных конструкций геометрического тела. По отношению линейных размеров обе пирамидальные составляющие октаэдра подобны таковым пирамиды Хуфу [3, 4, 5].

Основание обеих пирамидальных форм октаэдра содержит по четыре малых треугольника Кеплера и Фибоначчи, соприкасающихся в центре симметрии неправильного октаэдра одной из своих вершин (рисунок 14).

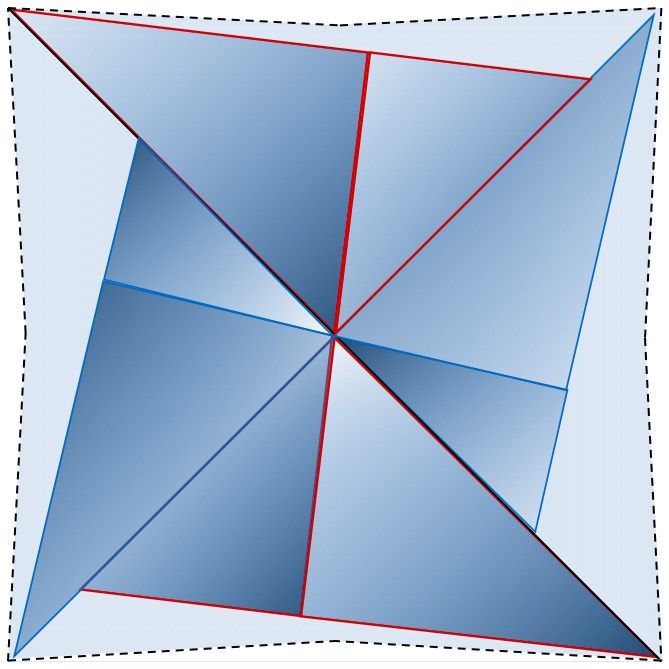
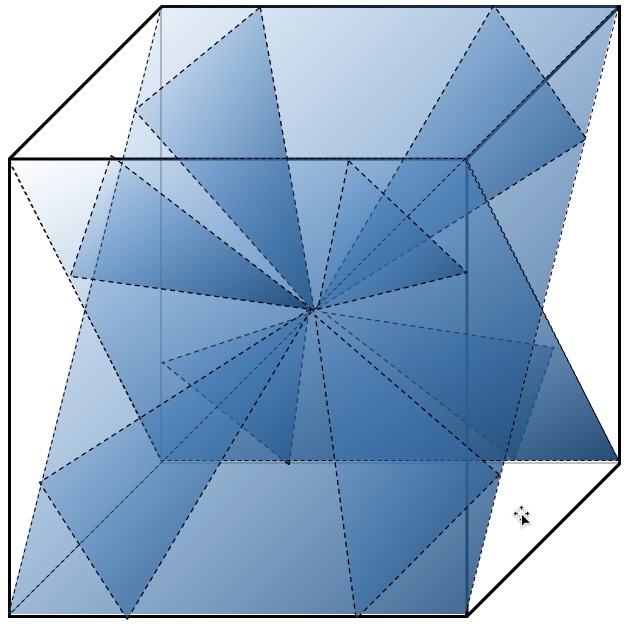
Построение куба. Построение геометрии куба посредством треугольников Кеплера и Фибоначчи требует 24 их пары. На рисунке 15 показано одно из шести подобных диагональных сечений куба, проходящее через его 4 вершины и центр симметрии. Вершины куба образованы соединением катетов треугольников Кеплера, гипотенузы которых являются общими с меньшими катетами треугольников Фибоначчи. Соединения катетов и гипотенуз треугольников Фибоначчи образуют центр симметрии куба.

Для наглядного представления геометрии куба и сечений с треугольниками Кеплера и Фибоначчи мы сделали рисунок двух диагональных сечений куба в трехмерной плоскости (рисунок 16). Мы сочли ненужным представление всех шести сечений куба в одном рисунке, так как подобное изображение будет очень сложным для восприятия.

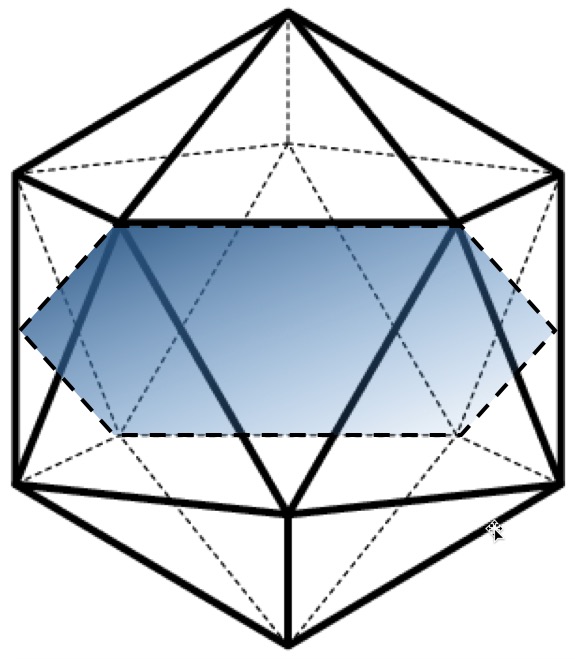
Построение икосаэдра. Существует возможность построения икосаэдра из шестидесяти пар треугольников Кеплера и Фибоначчи. Для наглядности при построении икосаэдра мы воспользовались его поперечным сечением, проходящим через его центр симметрии и четыре противоположных вершины (два ребра) [1] (рисунки 17, 18). Ребро икосаэдра образуют два малых катета треугольников Фибоначчи, а его вершины – соединения меньшего катета и гипотенузы треугольников Кеплера и Фибоначчи. Центр симметрии икосаэдра находится в месте соединения гипотенуз с катетами двух видов треугольников. Следует отметить в рассматриваемом сечении одно отношение: линейные размеры противолежащих ребер (вершин геометрического тела) и расстояние между ними равны константе Золотой пропорции. Икосаэдр содержит 30 ребер, следовательно, рассматриваемых нами сечений в нем – 15. Каждое подобное сечение содержит по 4 пары треугольников Кеплера и Фибоначчи. Общее количество треугольников икосаэдра, таким образом, равно 120.

Среди четырех платоновых тел – неправильные тетраэдр и октаэдр, куб, икосаэдр – имеется определенная числовая закономерность: отношение пар треугольников Кеплера и Фибоначчи в определенной нами геометрической структуре этих тел по порядку их усложнения (от тетраэдра, октаэдра и до куба) увеличивается ровно в два раза (6 пар – в тетраэдре, 12 пар – в октаэдре, 24 пары – в кубе), а увеличение количества пар элементов (треугольников Кеплера и Фибоначчи) между кубом и икосаэдром – ровно в 2,5 раза (24 пары и 60 пар).

Оси симметрии додекаэдра. Дуальный икосаэдру додекаэдр можно, так же как и икосаэдр, воспроизвести из 120 треугольников – 60-ти пар треугольников Кеплера и Фибоначчи. На рисунке 19 представлено сечение додекаэдра, проходящее через его центр симметрии и четыре противоположных вершины (два ребра) [1]. Рассматриваемое сечение позволяет разместить в нем четыре пары треугольников Кеплера и Фибоначчи с центром симметрии в середине геометрического тела. При этом общими для пар являются большие их катеты. Своими меньшими катетами они образуют непосредственно боковую линию сечения додекаэдра. Поперечное сечение додекаэдра, проходящее через его центр симметрии и четыре противоположных вершины (два ребра) позволяет выделить отношение Золотой пропорции между длиной ребра и расстоянием противолежащего ребра (рисунок 19, два прямоугольника выделенных красным и синим цветом). Рассматривая это сечение додекаэдра в трехмерной плоскости можно выделить так же отношение Золотого сечения между длиной ребра и расстоянием между двумя противолежащими вершинами одной поверхности додекаэдра (рисунок 20).

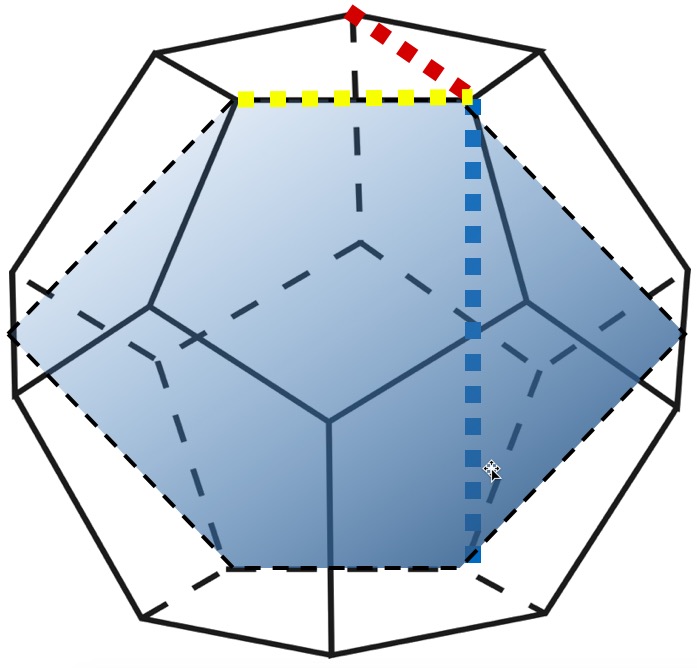
Красной, желтой, синей линией обозначены расстояния между отдельными вершинами. Вид сверху-спереди

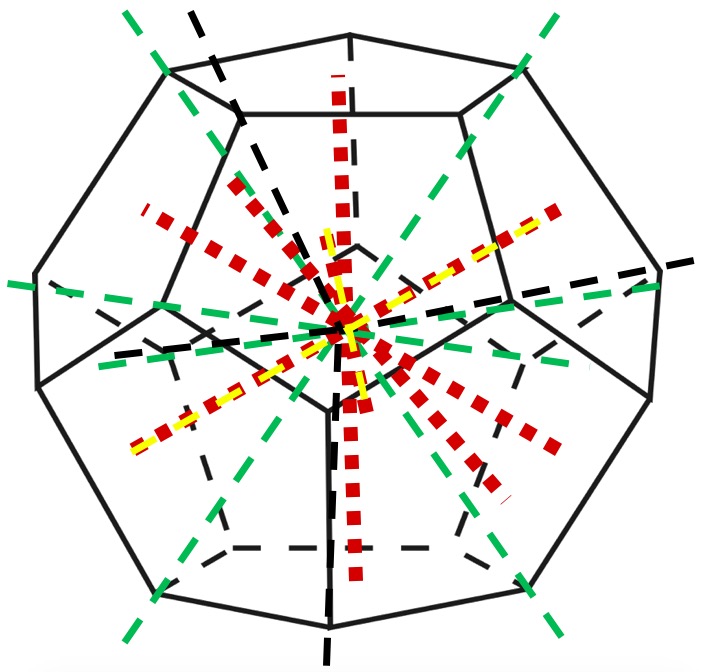
На рисунке 21 нами выделены оси симметрии вписанных в додекаэдр платоновых тел: красным и желтым цветом – оси симметрии всех вершин икосаэдра и четырех вершин куба; черным и зеленым – оси симметрии вершин тетраэдра и куба. Не выделены только в этом рисунке оси симметрии ребер для октаэдра (усложняет восприятие). Воспроизведенная нами геометрия четырех платоновых тел (тетраэдра, октаэдра, куба, икосаэдра) посредством треугольников Кеплера и Фибоначчи может быть вписана в додекаэдр определенными нами способами (совмещая центры симметрии тел с таковым додекаэдра) по отношению к выделенным осям симметрии додекаэдра (рисунок 22).

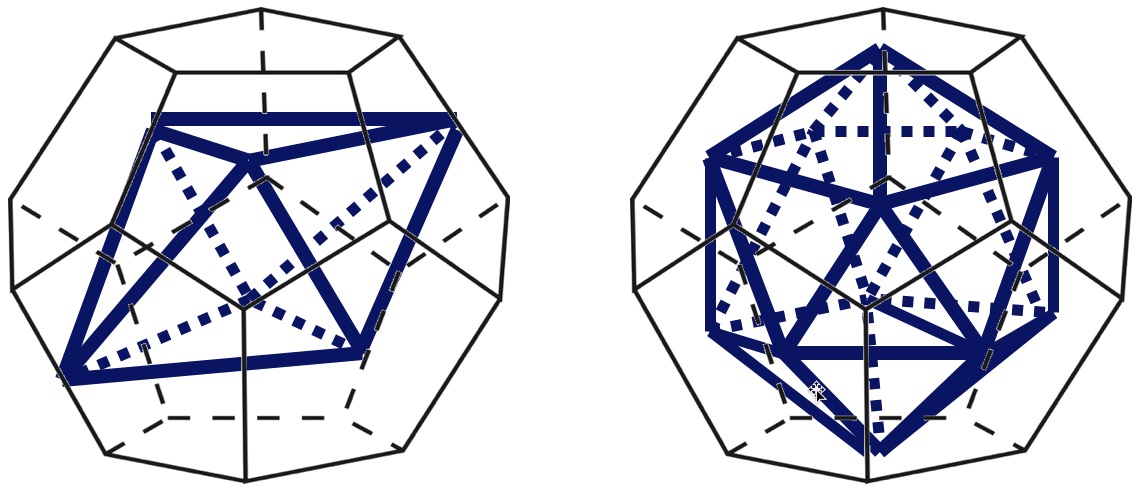
Вписывание неправильных геометрических тел в «правильную» геометрию додекаэдра может породить закономерный вопрос: если тела неправильны, то возможно ли их вписать в правильное геометрическое тело? Для прояснения вопроса вернемся к рисунку 20, где (в трехмерной плоскости) красной, желтой и синей линиями обозначены расстояния между отдельными вершинами. И эти расстояния соотнесены нами в пропорции Золотого сечения. А константа золотой пропорции – число иррациональное. На этом основании мы допускаем, что отношение линейных размеров додекаэдра не может быть точно определено. В этой связи мы признаем возможность вписывания в додекаэдр неправильных геометрических тел – построенных нами неправильного тетраэдра и неправильного октаэдра. Различия по высоте между правильным и неправильным тетраэдром составляют около 6 %, а различия по отношению к высоте соответствующего тетраэдру додекаэдра – и того меньше. Сопоставимые различия с различиями неправильного тетраэдра (по отношению к правильному тетраэдру) имеет и неправильный октаэдр. Оба рассматриваемых нами геометрических тела имеют поверхности (три у тетраэдра и восемь у октаэдра), образованные треугольниками и отличающиеся от таковых равностороннего треугольника на 1,7º – 58,3º.

В связи с проведенным исследованием, резюмируем: вписанные в геометрию платоновых тех дуальные треугольники Кеплера и Фибоначчи можно представить в виде математических отношений Золотой пропорции этих тел. Появляется возможность предположить, что наличие в структуре платоновых тел математических отношений Золотой пропорции в виде дуальных треугольников Кеплера и Фибоначчи может быть связано с его проявлением как структуро-, морфо- и функционально образующей материальной основы объектов неживой и живой природы. Подобная мысль, как представляется, перекликается с высказыванием С.Л. Василенко: «Если в глобальном проявлении окружающий мир упорядочен пропорциональными структурами, то велика вероятность, что в его основе лежит именно модель золотого сечения …золотая пропорция выступает в роли структурирующей подосновы»[2]

1. Алферов, С.А. О взаимосвязях додекаэдра и икосаэдра // «Академия Тринитаризма», М., Эл № 77-6567, публ.14041, 29.11.2006
2. Василенко, С.Л.Дуализм модели золотой пропорции // «Академия Тринитаризма», М., Эл № 77-6567, публ.23987, 23.11.2017
3. Ворон, А.В. Геометрический треугольник Фибоначчи и пирамида Хеопса // «Академия Тринитаризма», М., Эл № 77-6567, публ.23546, 13.07.2017
4. Ворон, А.В. Свойства треугольников Кеплера, Фибоначчи и их связь с геометрией пирамиды Хуфу // «Академия Тринитаризма», М., Эл № 77-6567, публ.24320, 04.03.2018
5. Ворон, А.В. Способ воспроизведения геометрии пирамиды Хуфу на основе использования чисел Фибоначчи // «Академия Тринитаризма», М., Эл № 77-6567, публ.24204, 20.01.2018
6. Платон. Тимей / Собр. соч. в 4-х т. – М.: Мысль, 1994.