«Книга природы написана на языке математики»
Г. Галилей
«Числа не управляют миром, но они показывают, как управляется мир»
И. Гёте
«Все, что находится в природе, математически точно и определенно»
М.В. Ломоносов
Аннотация. Показана возможность построения платоновых тел из структурных элементов – треугольников Кеплера (соотношение катетов 1:√1,618..) и Фибоначчи (соотношение катетов 1:1,618…) – при условии неизменности площади названных элементов. Количество элементов (или пар элементов) составляющих структуру «тетраэдра», «октаэдра», «куба» увеличивается, таким образом, в два раза, а «икосаэдра» – в пять раз по отношению к количеству элементов тетраэдра при неизменности показателя «площадь всех структурных элементов фигуры» и радиуса (r=3) вписанной в платоновы тела сферы. Кроме того, площадь структурных элементов двух додекаэдров (Sc.э.2дод.=√959 325) равна площади структурных элементов любых 5-ти платоновых тел, например, 5-ти тетраэдров (или октаэдров, кубов, икосаэдров) (Sc.э.1пл.т.=√38 373). Показанная возможность находится в соответствии с текстом произведения Платона «Тимей», согласно которому – платоновы тела могут «перерождаться друг в друга… ».
Ключевые слова: платоновы тела, структурированные геометрические объекты, структурные элементы, золотая пропорция, треугольник Кеплера, треугольник Фибоначчи, математическое тождество.
Введение
По результатам анализа геометрии одного из помещений пирамиды Хуфу «Камера Царя» выявлено, что линейные размеры пола помещения вмещают два прямоугольных треугольника со следующими свойствами: значение площади прямоугольного треугольника математически тождественно значению его периметра (P=27,4164078649986…), а так же – квадрата меньшего катета (27,4164078649986…≡Lм.кат.5,236067977499784…2) [3, 4] (математическое тождество – равенство, выполняющееся на всём множестве значений входящих в него переменных). В этой связи нами были определены возможные значения при тождестве площади и периметра у двумерных фигур, объема и площади – у трехмерных. На основании проведенного исследования, обобщая наблюдаемые значения тождеств в связи со значениями радиуса вписанной окружности, сформулирована теорема:
«в правильных двумерных и выпуклых трехмерных геометрических фигурах радиус вписанной окружности (радиус сферы для трехмерных фигур) при тождестве площади и периметра (площади и объема для трехмерныхфигур) одинаков (равен 2 для двумерных и 3 для трехмерных)»[4].
Кроме того, в одной из публикаций [2], нами показана возможность построения геометрии платоновых тел посредством двух треугольников, катеты которых обладают соотношением меры золотой пропорции – треугольника Кеплера (1:√Ф) и треугольника Фибоначчи (1:Ф). В статье показано, что «среди четырех платоновых тел (неправильные тетраэдр и правильные – октаэдр, куб, икосаэдр) имеется определенная числовая закономерность: количество пар треугольников Кеплера и Фибоначчи в определенной нами геометрической структуре этих тел по порядку их усложнения (от тетраэдра, октаэдра и до куба) увеличивается ровно в два раза (6 пар – в тетраэдре, 12 пар – в октаэдре, 24 пары – в кубе), а увеличение количества пар элементов (треугольников Кеплера и Фибоначчи) между кубом и икосаэдром – ровно в 2,5 раза (24 пары и 60 пар)» [2]. Результаты этого построения мы связали с информацией текста произведения «Тимей» [5]. Платон в своем произведении описывает ряд «перерождений» тел:
«…все четыре рода [тел] могут последовательно перерождаться друг в друга… …четыре рода действительно рождаются из выбранных нами треугольников… …не все роды могут разрешаться друг в друга и рождаться один из другого путем соединения большого количества малых [величин] в малое количество больших, и обратно»; «…вода, дробимая огнем или воздухом, позволяет образоваться одному телу огня и двум воздушным телам, равно как и осколки одной рассеченной части воздуха могут породить из себя два тела огня. Hо и наоборот, когда малая толика огня, оказавшись в больших толщах воздуха, воды или земли, подхватывается их движением, сокрушается в борьбе и дробится, два тела огня сплачиваются в единый вид воздуха; или когда воздух претерпевает насилие и разрушение, из двух его тел с половиной оказывается составлен один цельный вид воды» [5].
В этой связи нами сделано предположение:
для перехода (перерождения) платоновых тел друг в друга необходима некоторая постоянная величина (параметр) при прочих переменных. В качестве подобной величины (параметра) предполагается использовать параметр «площадь структурных элементов» (треугольников Кеплера и Фибоначчи), а в качестве переменной – их кратное количество в «структуре» платоновых тел.
Основная часть
Для проверки предположения сформулированы следующие задачи:
- исследовать возможность построения платоновых тел из структурных элементов – треугольников Кеплера и Фибоначчи – при условии неизменности площади названных элементов;
- показать возможность построения платоновых тел из структурирующих элементов – треугольников Кеплера и Фибоначчи и «перехода» (взаимопревращения) одних платоновых тел в другие, в различных вариациях;
- интерпретировать и обсудить полученные результаты исследования.
Для решения поставленных первых двух задач мы использовали геометрическое двухмерное плоскостное построение или, иначе говоря, геометрическое построение плоских фигур. Построенные структурированные геометрические объекты – платоновы тела «тетраэдр» и «октаэдр» – отличаются от их традиционного вида (представления) в том отношении, что они не являются правильными многогранниками (более подробно об этом в статье [2]).
Для построения платоновых тел «тетраэдр», «октаэдр», «куб», «икосаэдр» из структурных элементов – треугольников Кеплера и Фибоначчи – должны выполняться следующие условия (обозначенные нами ранее в статье [2]):
- построение геометрических тел (платоновых тел) допускается треугольниками Кеплера и Фибоначчи различных размеров, но не более трех;
- количество треугольников Кеплера и Фибоначчи должно быть одинаково (парно представлено в геометрии тел по количеству и их размерам);
- треугольники Кеплера и Фибоначчи должны образовывать центр симметрии построенного геометрического тела;
- треугольники Кеплера и Фибоначчи должны позволять формировать структурообразующие элементы геометрического тела: его вершины, грани и центр симметрии.
Кроме вышеназванных условий построения платоновых тел нами было обозначено еще одно исходное условие: для построения платоновых тел из структурных элементов – треугольников Кеплера и Фибоначчи – должны быть использованы параметры математической тождественности значений объема и площади этих геометрических фигур как исходные (таблица 1) [4]. При этом, в качестве единиц измерения длин и площадей структурных элементов, должны быть использованы условные единицы измерения (далее по тексту – у. е.). В качестве единицы измерения меры длины нами принята мера равная 1/3 части (=1 у.е.) радиуса вписанной в платоновы тела сферы (величина параметра «радиус вписанной сферы» неизменен).
![Таблица 1 – Математическое тождество значений объема и площади сферы и платоновых тел [4]](https://lah.ru/wp-content/uploads/2020/08/tabl.1-1000x389.png)
Построение неправильного тетраэдра (12 структурных элементов в 6 парах)
Для построения неправильного тетраэдра нами использовано шесть пар треугольников Кеплера и Фибоначчи различных размеров (по три больших и три малых треугольников Кеплера и Фибоначчи) (таблица 2).
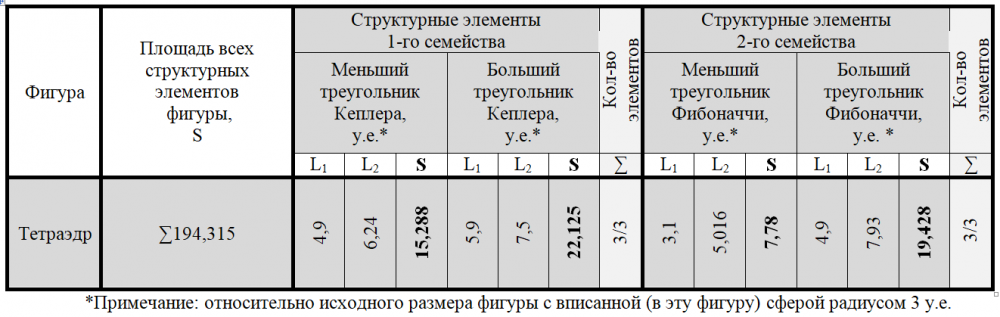
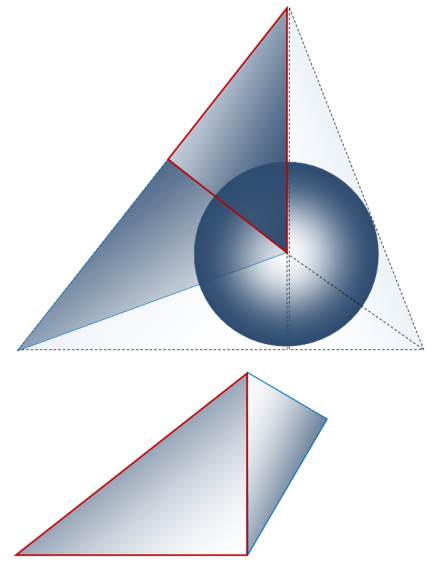
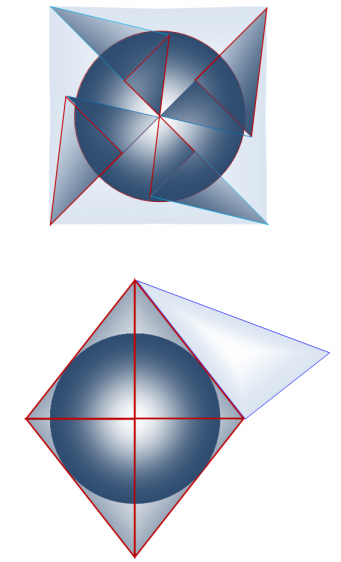
Гипотенузы трех меньших треугольников Кеплера одним своим концом соединены с вершиной тетраэдра, а другим – с центром симметрии тетраэдра. В свою очередь гипотенузы трех больших треугольников Фибоначчи (образующим пары с названными ранее треугольниками Кеплера) одним своим концом соединены с центром симметрии тетраэдра, а другим – с его вершиной (рисунки 1, 2). Образуемые таким образом пары треугольников соприкасаются друг с другом меньшими катетами. Гипотенузы же трех больших треугольников Кеплера соприкасаются с гипотенузами трех больших треугольников Фибоначчи, а гипотенузы трех меньших треугольников Фибоначчи – с меньшими катетами трех больших треугольников Кеплера под прямым углом (рисунки 1, 2).
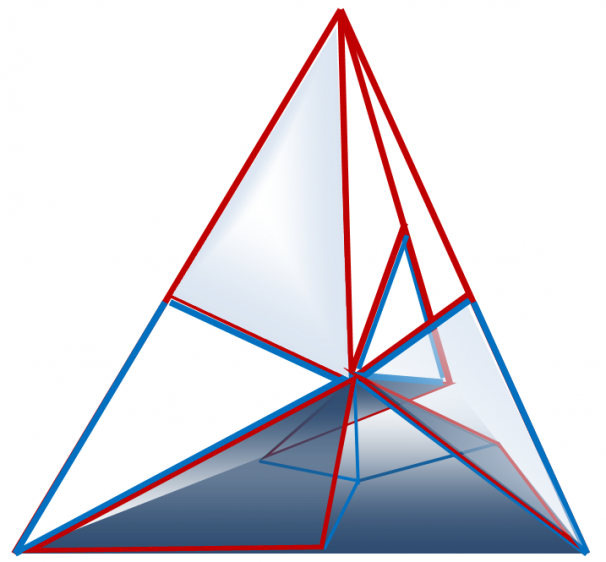
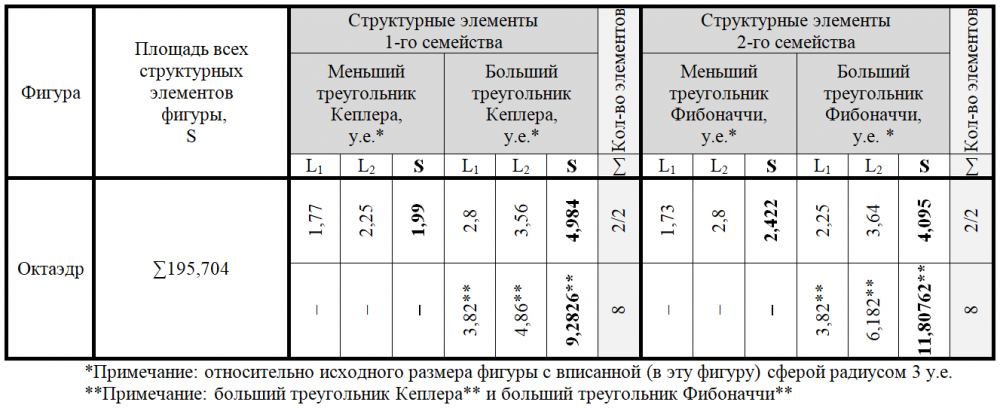
Построение неправильного октаэдра (24 структурных элемента в 12 парах)
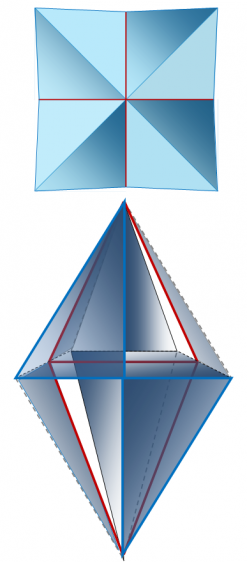
Для построения неправильного октаэдра понадобилось 12 пар треугольников Кеплера и Фибоначчи (таблица 3), (рисунки 3, 4). «Каркас» тела формируют 8 больших треугольников Кеплера** соприкасающихся между собой большими катетами в вертикальной плоскости и меньшими – в сагиттальной и горизонтальной плоскостях (крест-накрест) (рисунок 3, снизу). Восемь больших треугольников Фибоначчи** местами соединения гипотенуз и больших катетов образуют две противолежащих вершины тела, а меньшими своими катетами – периметр средней части и четыре вершины тела. Больший катет больших треугольников Фибоначчи** и гипотенузы больших треугольников Кеплера** образуют апофемы двух пирамидальных конструкций геометрического тела. «Внутреннюю» структуру неправильного октаэдра – проекция поперечного сечения в горизонтальной и сагиттальной плоскостях – образуют два меньших и больших треугольника Кеплера, а так же – два меньших и больших треугольника Фибоначчи (рисунок 3, сверху).
Построение правильного куба (48 структурных элемента в 24 парах)
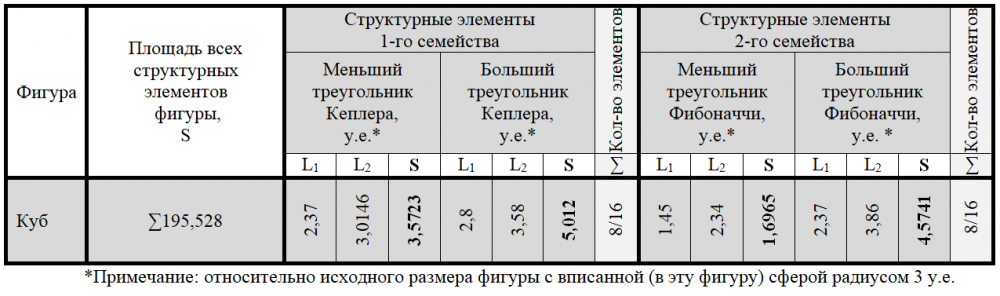
Построение геометрии куба посредством треугольников Кеплера и Фибоначчи требует 24 их пары. На рисунке 5 показано два варианта (из шести подобных этим двум) диагональных сечений куба, каждое из которых проходит через его 4 вершины и центр симметрии.
В первом варианте диагонального сечения куба (первый тип плоскости куба (всего 4 плоскости)) (рисунок 5, сверху) два больших и два меньших треугольников Кеплера соединены в одном случае гипотенузами с 2 большими треугольниками Фибоначчи, а в другом – гипотенузой с большим катетом большего треугольника Фибоначчи. Соединения больших катетов и гипотенуз треугольников Кеплера и Фибоначчи в этом варианте образуют центр симметрии куба.
Во втором варианте диагонального сечения куба (второй тип плоскости куба (всего 2 плоскости)) вершины куба образованы соединением катетов 4 меньших треугольников Фибоначчи, гипотенузы которых являются общими с меньшими катетами 4 больших треугольников Кеплера (рисунок 5, снизу). Соединения больших катетов и гипотенуз треугольников Кеплера в этом варианте образуют центр симметрии куба.
Общее количество структурных элементов куба, их размер (исходного размера фигуры с вписанной в нее сферой радиусом 3 у.е.) и их площадь представлены в таблице 4.
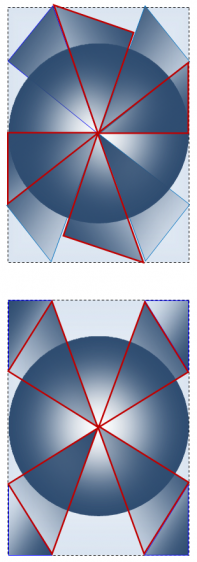
Для наглядного представления геометрии куба с треугольниками Кеплера и Фибоначчи мы представили рисунок двух диагональных сечений куба второго типа (рисунок 5, снизу) в трехмерной плоскости (рисунок 6). Мы сочли ненужным представление всех шести сечений куба в одном рисунке, так как подобное изображение окажется чрезмерно сложным для восприятия.
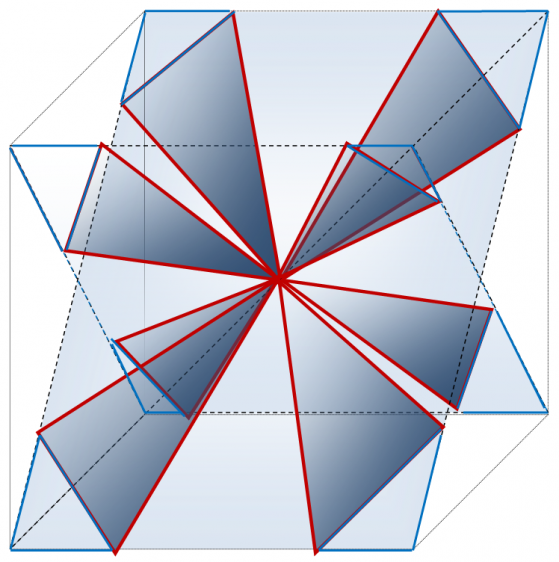
Построение правильного икосаэдра (60 структурных элементов в 30 парах)
Существует возможность построения икосаэдра из тридцати пар треугольников Кеплера и Фибоначчи. Для наглядности при построении икосаэдра мы воспользовались его поперечным сечением, проходящим через его центр симметрии и четыре противоположных вершины (два ребра) [1] (рисунки 7, 8). Ребра фигуры образованы меньшими катетами треугольников Кеплера и Фибоначчи. Вершины икосаэдра образуют соединения меньшего катета и гипотенузы двух треугольников Кеплера и – двух Фибоначчи (рисунки 7, 8). Центр симметрии икосаэдра находится в месте соединения гипотенуз с большими катетами двух видов треугольников. Икосаэдр содержит 30 ребер, следовательно, рассматриваемых нами сечений в нем – 15. Каждое сечение содержит по 2 пары треугольников Кеплера и Фибоначчи. Общее количество структурных элементов икосаэдра, таким образом, – равно 60 (таблица 5).
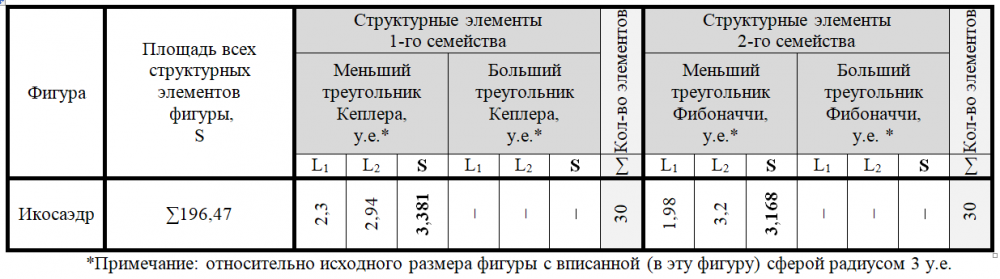
![Рисунок 7 – Поперечное сечение икосаэдра, проходящее через его центр симметрии и четыре противоположных вершины (два ребра) [1]. Треугольники Кеплера обозначены красным цветом, треугольники Фибоначчи – синим](https://lah.ru/wp-content/uploads/2020/08/ris.7-582x562.png)
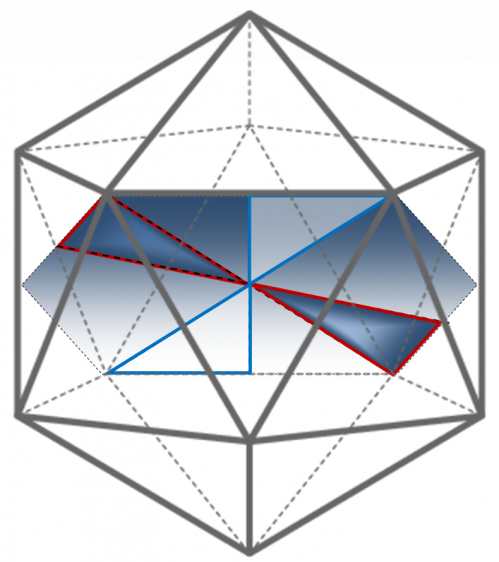
Построение правильного додекаэдра (240 структурных элементов в 120 парах)
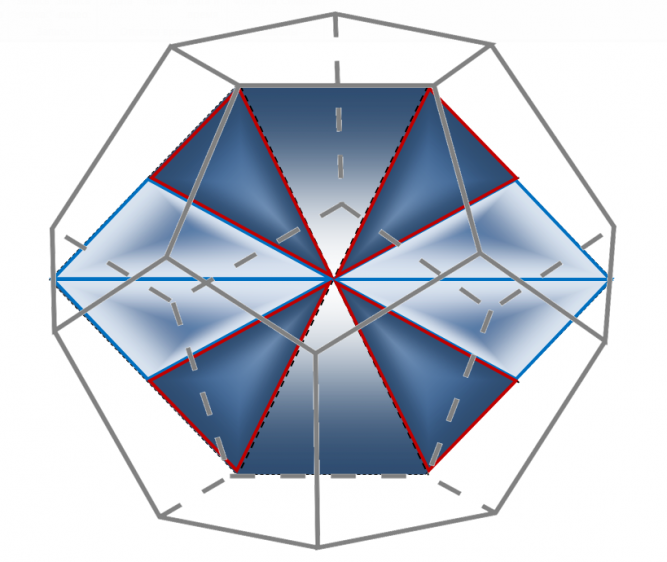
Дуальный икосаэдру додекаэдр можно воспроизвести из 240 треугольников – 60-ти пар треугольников Кеплера и Фибоначчи (таблица 6). На рисунках 9, 10 представлено сечение додекаэдра, проходящее через его центр симметрии и четыре противоположных вершины [1]. Рассматриваемое сечение позволяет разместить в нем четыре пары больших треугольников Кеплера и Фибоначчи с центром симметрии в середине геометрического тела (4*15=60). При этом общими для пар – больших треугольников Кеплера и Фибоначчи – являются их большие катеты. Своими меньшими катетами они образуют линию сечения додекаэдра (его ребра). Меньшие треугольники Кеплера и Фибоначчи образуют грани додекаэдра: каждая из 12 граней фигуры содержит по 5 пар меньших треугольников Кеплера и Фибоначчи (12*5=60). Треугольники пар соприкасаются большими катетами, а меньшими катетами – образуют ребра фигуры (рисунок 9).
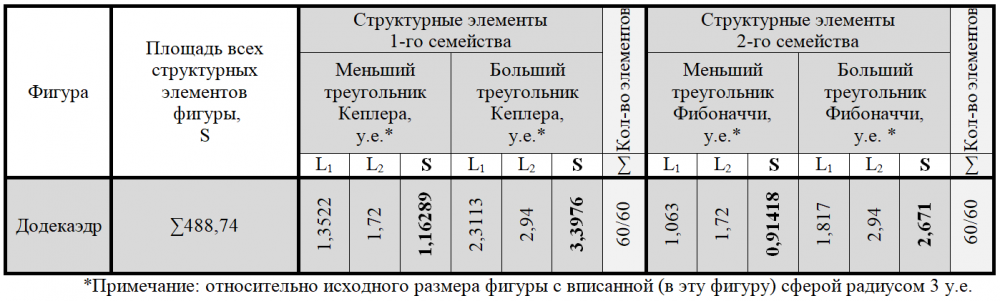
![Рисунок 9 – Поперечное сечение додекаэдра, проходящее через его центр симметрии и четыре противоположных вершины (два ребра) [1]. Треугольники Кеплера обозначены красным цветом, треугольники Фибоначчи – синим](https://lah.ru/wp-content/uploads/2020/08/ris.9-372x562.png)
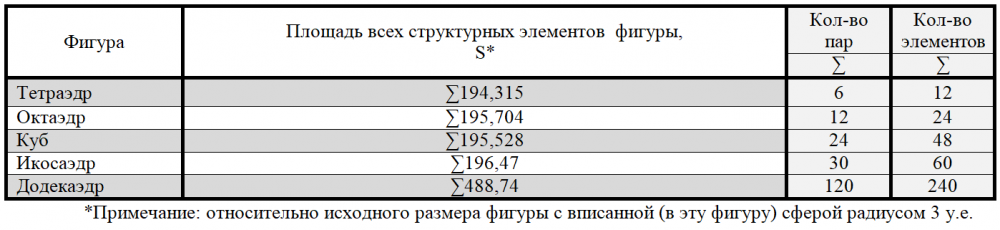
Опыт построения платоновых тел (их геометрической структуры из структурных элементов) свидетельствует о возможности создания этих геометрических фигур посредством структурных элементов – треугольников Кеплера и Фибоначчи – при условии неизменности площади названных элементов. Количество элементов (или пар элементов) составляющих структуру «тетраэдра», «октаэдра», «куба» увеличивается, таким образом, в два раза, а «икосаэдра» – в пять раз по отношению к количеству элементов тетраэдра при неизменности показателя «площадь всех структурных элементов фигуры» (таблица 7).
Кроме того, были найдены следующие закономерности при построении платоновых тел посредством элемнтов структуры:
- в сумме площадь всех структурных элементов любого из четырех платоновых тел – «тетраэдра», «октаэдра», «куба», «икосаэдра» – соотносится к площади (тождественна его объему) вписанной сферы (с радиусом 3) в эти геометрические фигуры как √3:1 (≈195,8902754094751 и 113,0973032392904);
- площадь элементов каждого из четырех платоновых тел – «тетраэдра», «октаэдра», «куба», «икосаэдра» – очень близка к значению 195,8902754094751=√38 373.
Таким образом: √3*√12791 (√12791=113,0973032392904 – значение площади сферы) = 195,8902754094751=√38 373. Значения числа √38 373 и √12791 соотносятся как 3:1 – это отношение значения площади элементов любого из четырех Платоновых тел (тетраэдра, октаэдра, куба, икосаэдра) к значению площади сферы с радиусом 3. Таким образом: площадь элементов каждого из четырех платоновых тел – тетраэдра, октаэдра, куба, икосаэдра – соотносится к площади (или объему) вписанной в эти четыре тела сферы как √3:1.
Как уже было показано, среди четырех платоновых тел – неправильные тетраэдр и октаэдр, куб, икосаэдр – имеется определенная числовая закономерность: отношение пар треугольников Кеплера и Фибоначчи в определенной нами геометрической структуре этих тел (по порядку их усложнения от тетраэдра, октаэдра и до куба): 6 пар – в тетраэдре, 12 пар – в октаэдре, 24 пары – в кубе, 30 пар в икосаэдре, 120 пар в додекаэдре. Таким образом, если брать за единицу отсчета количество пар додекаэдра (120 пар=240 элементов), то количество этих пар будет кратно количеству элементов 20 тетраэдров, 10 октаэдров, 5 кубов, 4 икосаэдра. В то же время, площадь элементов тетраэдра, октаэдра, куба, икосаэдра одинакова и равна значению √3 помноженное на значение площади вписанной окружности.
Из площади структурных элементов двух додекаэдров (Sc.э.2дод.=√959 325) можно получить площадь равную площади структурных элементов любых 5-ти платоновых тел, например, 5-ти тетраэдров или октаэдров, кубов, икосаэдров… и так далее (Sc.э.пл.т.=√38 373).
Значение площади и тождественное значение объема вписанной в платоновы тела сферы (113,0973032392904) кратно значению меры «Королевский кубит» [3], а получаемое в этом случае кратное значение – 216 (1) – равно значению тождества объема и площади куба (см. таблицу 1) [4].
113,0973032392904/0,523606797749979=216 (1)
Высказанное нами предположение о возможности переходов (перерождения) платоновых тел друг в друга (при некоторой постоянной величине (параметре) при прочих переменных) оказалась практически реализуемым при постоянной величине (параметре) «площадь структурных элементов», а в качестве переменной – их кратное количество в «структуре» платоновых тел.
Интерпретация и обсуждение результатов исследования
Учитывая, что описанное математическое тождество площади, объема и одинаковый радиус вписанной окружности наблюдается только у трехмерных фигур – платоновых тел (которые могут быть построены из двух типов треугольников обладающих соотношением меры золотой пропорции) можно предположить (следуя методологическому принципу «Бритва Оккама»), что в качестве универсальных мер Природы, обеспечивающих целостность и соразмерность всех ее систем, могут выступить:
- мера золотой пропорции, основанная на принципе сравнения (соотношения не более двух величин) и проявляемая в виде двух структурообразующих треугольников и обладающих соотношением меры золотой пропорции – Кеплера и Фибоначчи;
- мера тождественности значений параметров платоновых тел и непосредственно проявляемая в виде тождественности значений площади и объема, равенства значений радиуса вписанной сферы этих геометрических объектов.
Каким же образом, учитывая вышесказанное, возможно объяснить реальное проявление (реализацию) в физических материальных объектах меры золотой пропорции и тождественности параметров платоновых тел? В дальнейшем обсуждении, чтобы дать более-менее определенный ответ, невозможно (на наш взгляд) обойтись без использования концепций или теорий метафизического характера. Например, теории мировой среды.
Следует отметить, что в произведении Платона «Тимей», где философ излагает свою космологию, слово «правдоподобно» и «правдоподобие» встречается 19 раз. По определению, правдоподобие – сходство с правдой, истиной. И в то же в произведении, в контексте изложения о правдоподобном, встречается часто слово «миф» – 5 раз. Подчеркивается героем повествования, что сказанное специально облачено в форму мифа и оно, по-возможности, соответствует истине в рамках меры правдоподобия: «… мы, рассматривая во многих отношениях много вещей, таких, как Боги и рождение Вселенной, не достигнем в наших рассуждениях полной точности и непротиворечивости. Напротив, мы должны радоваться, если наше рассуждение окажется не менее правдоподобным, чем любое другое, и притом помнить, что и я, рассуждающий, и вы, мои судьи, всего лишь люди, а потому нам приходится довольствоваться в таких вопросах правдоподобным мифом, не требуя большего»; «… у этого сказания облик мифа, но в нем содержится и правда …». Герой произведения поясняет свой выбор изложения в форме правдоподобного мифа следующими доводами: «…при избранном нами способе исследования затруднительно было бы привести наши мысли … в должную ясность. Поэтому ни вы не должны требовать от меня последнего слова на этот счет, ни я не могу убедить себя, что поступлю правильно, если взвалю на себя такую задачу. Напротив, я намерен и здесь придерживаться того, что обещал в самом начале, а именно: пределов вероятного, и попытаюсь, идя от начала, сказать обо всем в отдельности и обо всем вместе такое слово, которое было бы не менее, а более правдоподобным, нежели любое иное» [5]. В этой связи следует воспринимать написанное Платоном в «Тимее» как некое мифическое, но в то же время правдоподобное повествование, в котором существует правдивое знание в форме мифа, сказки…
Платон, повествуя о Вселенной, сообщает о трех родах или вещах: «… во-первых, об основополагающем первообразе, который обладает мыслимым и тождественным бытием, а во-вторых, о подражании этому первообразу, которое имеет рождение и зримо. В то время мы не выделяли третьего вида … . Какую же силу и какую природу припишем мы ему? Прежде всего вот какую: это – восприемница и как бы кормилица всякого рождения» [5].
Что же подразумевалось в «Тимей» под словами «Восприемница» и «Кормилица»? В последующем тексте мы не раз встречаем эти слова во вполне определенном контексте. Вот, к примеру, в таком: «…о Кормилице рождения скажем вот что: поскольку она и растекается влагой, и пламенеет огнем, и принимает формы земли и воздуха, и претерпевает всю чреду подобных состояний, являя многообразный лик, и поскольку наполнявшие ее силы не были ни взаимно подобны, ни взаимно уравновешены и сама она ни в одной своей части не имела равновесия, она повсюду была неравномерно сотрясаема и колеблема этими силами и в свою очередь сама колебала их своим движением. … Вот наподобие этого и четыре упомянутых рода были тогда колеблемы Восприемницей, которая в движении своем являла собой как бы сито: то, что наименее сходно между собой, она разбрасывала дальше всего друг от друга, а то, что более всего сходно, просеивала ближе всего друг к другу; таким образом, четыре рода обособились в пространстве еще до того, как пришло время рождаться устрояемой из них Вселенной» [5].
Из вышесказанного можно предположить, что под словами «Восприемница» и «Кормилица» вероятно подразумевалась мировая среда (эфир), а под платоновыми телами (четыре рода) – наименьшие из элементарных частиц – фундаментальные частицы. Таким образом, платоновы тела (фундаментальные частицы) могут обладать свойством взаимного перехода (перерождения) и некоторым образом – быть связанными с мировой средой (эфиром). Каким же образом может быть обеспечена эта связь? Обратимся в этой связи к высказыванию В.И. Ленина, которое он сделал в своей главной работе по философии «Материализм и эмпириокритицизм. Критические заметки об одной реакционной философии» где указывает: «Как ни диковинно с точки зрения “здравого смысла” превращение невесомого эфира в весомую материю и обратно … – … это только лишнее подтверждение диалектического материализма». Именно от этого высказывания и будем исходить в дальнейших логических построениях.
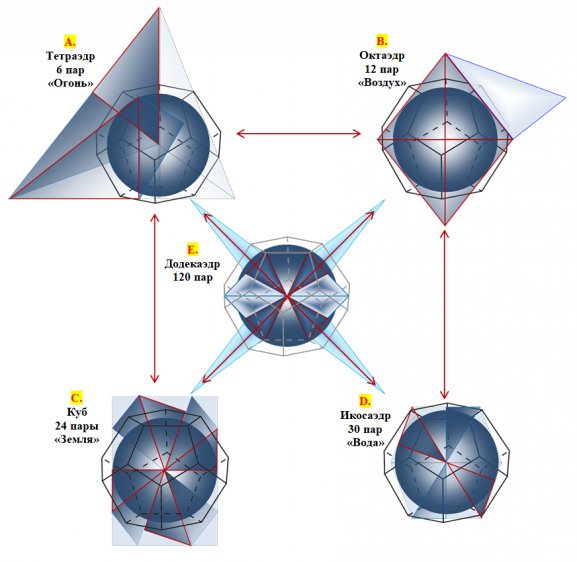
Итак: платоновы тела (фундаментальные частицы) могут «перерождаться» друг в друга и, в то же время, – непосредственно физически проявляться в результате «превращения» мировой среды (эфира) в материю (частицы). Исходя из существующих модельных представлений о мировой среде [2] (рисунок 11) и выявленных в данном исследовании возможностях взаимного перехода платоновых тел можно наглядно представить появление и взаимный «переход» платоновых тел (рисунок 12). Согласно нашим представлениям – из двух элементов (тел 2 додекаэдров) додекаэдрового поля (составляющего мировую среду) может возникнуть 5 элементов (5 тел) любого из четырех платоновых тел «тетраэдр», «октаэдр», «куб», «икосаэдр».

Радиус вписанной сферы в платоновы тела одинаков, а значит – при наличии неизменной величины параметра – можно предположить, что, кроме взаимного «перехода» одного тела в другое возможно и движение тел в среде, названной нами в публикации [2] как «додекаэдровое поле» (мировая среда). На рисунке 13 показана модель «додекаэдрового поля» состоящая из элементов-сфер и вписанных в это «додекаэдровое поле» (см. рисунок 11). Моделирование условий различного расположения сфер у модели додекаэдрового поля показало возможность их подвижности относительно друг друга в двух направлениях – вертикальном (рисунок 13, вверху) и горизонтально-сагиттальном (рисунок 13, внизу). В первом случае соприкасаются радиально расположенные сферы, а во втором – вертикально расположенные.

Предполагаемые способ движения тел в среде додекаэдрового поля – квантовый переход – мгновенное перемещение (квантом движения) вписанных в додекаэдровое поле четырех платоновых тел – «тетраэдр», «октаэдр», «куб», «икосаэдр» – в среде поля. Подобное перемещение, в этом случае, возможно лишь при единичном движении частиц-тел (отдельных фундаментальных частиц) или при условии их объединения в группы со строго определенными композициями, которые позволяют «вписаться» в поле среды.
Возможные композиции частиц-тел (отдельных фундаментальных частиц) представлены моделями платоновых тел (рисунок 14).

Нами определены возможные композиции моделей фундаментальных частиц (соединения вершинами фигур, местами граней с совпадением их вершин, местами граней по периметру относительно центра симметрии комплекса фигур):
– икосаэдр+тетраэдр соединены вершинами (рисунок 15, слева);
– октаэдр+тетраэдр соединены вершинами (рисунок 15, справа);
– тетраэдр+тетраэдр соединены гранями (рисунок 16, слева),
– тетраэдр+тетраэдр соединены вершинами (рисунок 16, справа);
– куб+куб… соединены гранями (рисунок 17, слева),
– икосаэдр+икосаэдр… соединены гранями (рисунок 17, справа);
– октаэдр+октаэдр+октаэдр+октаэдр+октаэдр соединены гранями (рисунок 18, слева);
– икосаэдр+икосаэдр+икосаэдр+икосаэдр+икосаэдр соединены гранями (рисунок 18, справа).
Построение различных композиций платоновых тел (в процессе создания моделей фундаментальных частиц в соответствии с «правилам» их нахождения в додекаэдровом поле) позволяет «порождать» значительное разнообразие оригинальных соединений.




Заключение
- Показана возможность построения платоновых тел из структурных элементов – треугольников Кеплера (соотношение катетов 1:√1,618..) и Фибоначчи (соотношение катетов 1:1,618…) – при условии неизменности площади названных элементов. Количество элементов составляющих структуру «тетраэдра», «октаэдра», «куба» увеличивается, таким образом, в два раза, а «икосаэдра» – в пять раз по отношению к количеству элементов тетраэдра при неизменности показателя «площадь всех структурных элементов фигуры» (Sc.э.1пл.т.=√38 373) и радиуса (r=3) вписанной в платоновы тела сферы.
- Площадь структурных элементов двух додекаэдров (Sc.э.2дод.=√959 325) равна площади структурных элементов любых 5-ти платоновых тел, например, 5-ти тетраэдров, октаэдров, кубов, икосаэдров (Sc.э.1пл.т.=√38 373). Показанная возможность находится в соответствии с текстом произведения Платона «Тимей», согласно которому платоновы тела могут «перерождаться друг в друга… ».
- В связи с результатами настоящего исследования и содержанием произведения Платона «Тимей» сделано предположение: что под словами «Восприемница» и «Кормилица» подразумевалась мировая среда, а под платоновыми телами – фундаментальные частицы, которые, таким образом, могут обладать свойствами взаимного перехода (перерождения) и движения в этой среде.
- Определены возможные композиции моделей фундаментальных частиц в пространстве «додекаэдрового поля». Показано, что построение различных композиций платоновых тел (в процессе создания моделей фундаментальных частиц в соответствии с «правилам» их нахождения в додекаэдровом поле) позволяет «порождать» значительное разнообразие их оригинальных соединений.
Список литературы:
- Алферов, С.А. О взаимосвязях додекаэдра и икосаэдра // «Академия Тринитаризма», М., Эл № 77-6567, публ.14041, 29.11.2006.
- Ворон, А.В. Дуальность и комплементарность треугольников Кеплера, Фибоначчи и их связь с геометрией платоновых тел // «Академия Тринитаризма», М., Эл № 77-6567, публ.24401, 06.04.2018.
- Ворон, А.В. Мера длины «Королевский кубит» и позиционная система счисления с иррациональным основанием // «Академия Тринитаризма», М., Эл № 77-6567, публ.25842, 01.11.2019.
- Ворон, А.В. Тождество значений площади и периметра ряда двумерных фигур, объема и площади – трехмерных // «Академия Тринитаризма», М., Эл № 77-6567, публ.25873, 14.11.2019.
- Платон. Тимей / Собр. соч. в 4-х т. Т 3. – М.: Мысль, 1994. – 654 с.














Добавить комментарий